The article “How to Create Complex Paths in SVGs” examined the <path> element and showed how to draw a series of lines and arcs to create any shape. (It’s often used to replicate fonts without requiring a full font download.)
The d attribute offers a couple of extra tricks to draw smooth curves. In this article, we’ll discuss quadratic Bézier curves, but you can also refer to “How to Draw Cubic Bézier Curves on SVG Images” for a more complex option.
What are Quadratic Bézier Curves?
A quadratic curve has a start point (P0) and end point (P2). A single control point (P1) determines the curvature of the line. Wikipedia’s Bézier curve page provides a good generation illustration:
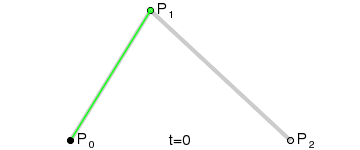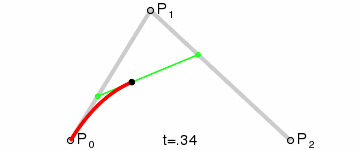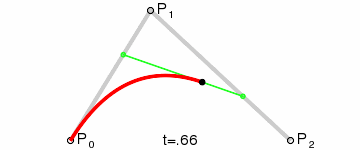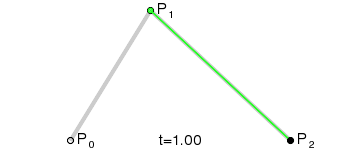
Math ninjas can also examine the migraine-inducing equations at WolframMathWorld.
Quadratic curves are great for drawing smooth edges. As you can see from this image, it’s easy to specify a control point where a squared edge would normally appear:
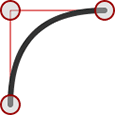
Perplexing Paths
Quadratic Bézier curves are defined using a Q directive in the SVG path d attribute:
<path d="M100,250 Q250,100 400,250" />
The initial M directive moves the pen to the first point (100,250). Two coordinates follow the Q: the single control point (250,100) and the final point being drawn to (400,250).
You can also use a lowercase q to denote relative rather than absolute coordinates. The following curve would be identical and is possibly easier to code:
<path d="M100,250 q150,-150 300,0" />
Finally, there are shorthand T and t directives (as usual, the lowercase option denotes relative rather than absolute coordinates). These accept further ending coordinates to string multiple curves together. The control point is inferred from the last used to guarantee a perfectly smooth continuing curve. For example, take this path:
<path d="M100,250 Q250,100 400,250 T700,250" />
It draws a curve from 100,250 to 400,250 with a control point at 250,100. A further curve is drawn ending at 700,250 and the control point is inferred to be 550,400.
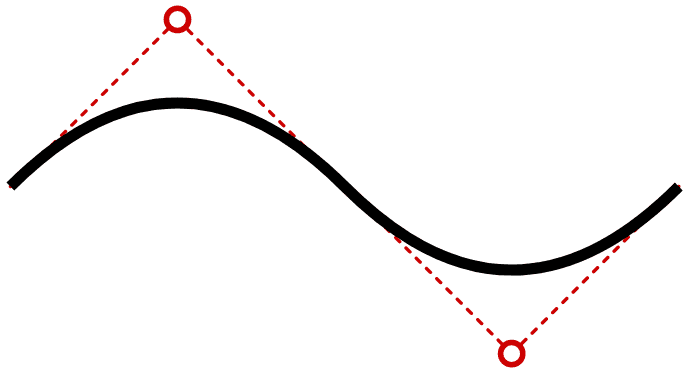
The inferred control point will be mathematically correct but may not always be what you require!
Quadratic Bézier curves can be a little difficult to code and visualize, so this quick generation tool will generate the <path> code for you:
See the Pen SVG quadradic bézier curve path creation tool by SitePoint (@SitePoint) on CodePen.
Drag the control point at either end of the curve accordingly. Click the curve itself to toggle a fill effect which adds an ending Z directive.
Note that this tool must convert DOM page coordinates to SVG coordinates to ensure it works at all screen sizes. This can be a little more complex than you expect, so refer to “How to Translate from DOM to SVG Coordinates and Back Again” for full details.
If you’re ready to tackle something more complex, try creating cubic Bézier curves on SVG images.
Frequently Asked Questions (FAQs) about HTML5 SVG Quadratic Curves
What is the difference between SVG quadratic curves and cubic curves?
SVG quadratic curves and cubic curves are both types of Bezier curves used in vector graphics. The main difference between them lies in the number of control points they use. Quadratic curves use two control points – one for the start, one for the end, and one control point to define the curve’s shape. On the other hand, cubic curves use four control points – two for the start and end points, and two additional control points to define the curve’s shape. This gives cubic curves more flexibility and complexity in the shapes they can create compared to quadratic curves.
How can I create a smooth curve using SVG quadratic curves?
Creating a smooth curve using SVG quadratic curves involves careful placement of the control points. The ‘Q’ command in SVG path data can be used to create a quadratic Bezier curve. The command takes two parameters: the coordinates of the control point and the coordinates of the end point. By adjusting these parameters, you can create a smooth curve. It may take some trial and error to get the curve exactly as you want it, as the placement of the control point can significantly affect the curve’s shape.
Can I use SVG quadratic curves to create complex shapes?
Yes, SVG quadratic curves can be used to create complex shapes. While a single quadratic curve might be limited in the shapes it can create, combining multiple curves can result in more complex shapes. By adjusting the control points and end points of each curve, you can create a variety of shapes. However, for very complex shapes, you might find cubic curves or a combination of quadratic and cubic curves more suitable.
How can I animate SVG quadratic curves?
SVG provides several ways to animate elements, including quadratic curves. One common method is to use the ‘animate’ element, which can change an attribute of an element over time. For example, you could animate the control point of a quadratic curve to make the curve appear to move. Another method is to use CSS animations or JavaScript to change the attributes of the SVG element.
Why are my SVG quadratic curves not displaying correctly?
There could be several reasons why your SVG quadratic curves are not displaying correctly. One common issue is incorrect syntax in the path data. Make sure that your ‘Q’ commands are followed by the correct number of parameters and that the parameters are valid coordinates. Another issue could be incorrect placement of the control points, which could result in the curve not appearing as expected. If you’re still having trouble, it might be helpful to use an SVG editor or validator to check your code.
Can I use SVG quadratic curves in responsive design?
Yes, SVG quadratic curves can be used in responsive design. SVG is inherently scalable, meaning it can adjust to different screen sizes without losing quality. You can control the size and position of your curves using CSS or by adjusting the ‘viewBox’ attribute of the SVG element. This allows you to create designs that adapt to different screen sizes and resolutions.
How can I fill the area under an SVG quadratic curve?
You can fill the area under an SVG quadratic curve by using the ‘fill’ attribute. This attribute sets the color of the area enclosed by the path. By default, the fill is black. You can set it to any color you like using CSS color values. If your path is not closed, you will need to close it by adding a ‘Z’ command at the end of your path data.
Can I use gradients with SVG quadratic curves?
Yes, you can use gradients with SVG quadratic curves. SVG provides ‘linearGradient’ and ‘radialGradient’ elements that you can use to create gradient fills. You can apply these gradients to your curves by setting the ‘fill’ attribute to the ID of the gradient.
How can I add text along an SVG quadratic curve?
SVG provides the ‘textPath’ element, which allows you to place text along a path, including quadratic curves. To do this, you first need to define your path and give it an ID. Then, you can use the ‘textPath’ element to add text, referencing the path by its ID.
Can I interact with SVG quadratic curves using JavaScript?
Yes, you can interact with SVG quadratic curves using JavaScript. SVG elements are part of the DOM, so you can manipulate them using JavaScript just like any other HTML element. This allows you to create interactive graphics, such as changing the shape of a curve in response to user input.
Craig BucklerCraig is a freelance UK web consultant who built his first page for IE2.0 in 1995. Since that time he's been advocating standards, accessibility, and best-practice HTML5 techniques. He's created enterprise specifications, websites and online applications for companies and organisations including the UK Parliament, the European Parliament, the Department of Energy & Climate Change, Microsoft, and more. He's written more than 1,000 articles for SitePoint and you can find him @craigbuckler.
