Data Structures for PHP Devs: Trees

In a previous article I introduced two basic data structures: stack and queue. The article was well received so I’ve decided to share data structures in an intermittent on-going series here at SitePoint. In this entry I’ll introduce you to trees, another data structure used in software design and architecture. More articles and data structures will follow!

Key Takeaways

• Tree data structures in PHP are hierarchical, implying a parent-child relationship between nodes, and are beneficial for representing hierarchical relationships, organizing data, and facilitating efficient search and sort operations.
• Tree traversal in PHP involves visiting each node in the tree data structure once. The three common methods are pre-order, in-order, and post-order traversal.
• Implementing a tree data structure in PHP involves creating a class for the tree nodes. Each node will have a value and an array to hold its children. You can then create methods to add and remove nodes, as well as to traverse the tree.
• Balancing a tree in PHP involves rearranging the nodes so that the depth of the left and right subtrees of every node differs by at most one. This can be achieved using various algorithms, such as the AVL or Red-Black tree algorithms. Balancing a tree can improve the efficiency of search operations.

A Search Problem

Data structure management generally involves 3 types of operations:

• insertion – operations that insert data into the structure.
• deletion – operations that delete data from the structure.
• traversal – operations that retrieve data from the structure.

In the case of stacks and queues, these operations are position-oriented – that is, they are limited by the position of the item in the structure. But what if we needed to store and retrieve data by its value?

Consider the following list (arranged in no particular order):

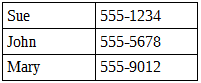
Clearly neither a stack nor queue would be suitable; we would potentially have to traverse the entire structure in order to find a particular entry if the value is either the last in the list or is not in the list at all. Assuming that the required value is in the list, and that each item is equally likely to contain the required value, we would need to visit an average of n/2 items – where n is the length of the list. The longer the list, the longer it will take to find what we’re looking for. What is required in this instance is the ability to arrange the data in a way that facilitates searching, which is where trees come in.

We can abstract this data as a “table” with the following basic operations:

• create – create an empty table.
• insert – add an item to the table.
• delete – remove an item from the table.
• retrieve – find an item in the table.

If this looks vaguely similar to database Create, Read, Update, Delete (CRUD) operations, that’s because trees are intimately related to databases and and how they represent data records internally.

One way we can represent our “table” is as a linear implementation – such that it mirrors the flat, list-like appearance of a table. Linear implementations can either be sorted or unsorted, and sequential (i.e. fixed-length records or variable-length using record delimiters) or linked (using record pointers). For what it’s worth, early database designs such as IBM’s Indexed Sequential Access Method (ISAM) and legacy file systems such as MS-DOS’s File Allocation Table (FAT) were based on linear implementations.

The downside of sequential implementations is that they are more expensive in terms of inserts and deletes, whereas linked implementations allow for dynamic storage allocation. Searching a fixed-length sequential implementation however is considerably more efficient than a linked implementation since it can more easily facilitate a binary search.

Trees

So as we’ve learned, sometimes it may be more efficient to use a non-linear search implementation such as a tree. Trees provide the best features of both sequential and linked table implementations and support all table operations in a very efficient manner. For this reason, many modern databases and file systems now use trees to facilitate indexing. For example, MySQL’s MyISAM storage engine uses Trees for indices, and Apple’s HFS+, Microsoft’s NTFS, and btrfs for Linux all use trees for directory indexing.

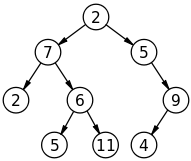
As you can see, trees are typically hierarchical and imply a parent-child relationship between the nodes. A node with no parents is called the root, and a node with no children is called a leaf. Child nodes of the same parent are called siblings. The term edges refers to the connections (indicated by arrows) between nodes.

You’ll note that the binary tree in the figure above is a variation of a doubly-linked list. In fact, if we rearranged the nodes to flatten the tree it would look exactly like a doubly-linked list!

A node with at most two children is the simplest form of a tree, and we can utilize this property to construct a binary tree as a recursive collection of binary nodes:

<?php
class BinaryNode
{
    public $value;    // contains the node item
    public $left;     // the left child BinaryNode
    public $right;     // the right child BinaryNode
    public function __construct($item) {
        $this->value = $item;
        // new nodes are leaf nodes
        $this->left = null;
        $this->right = null;
    }
}
class BinaryTree
{
    protected $root; // the root node of our tree
    public function __construct() {
        $this->root = null;
    }
    public function isEmpty() {
        return $this->root === null;
    }
}

Inserting Nodes

Adding items to a tree is a little more “interesting”. There are several solutions – many of which involve rotating and rebalancing the tree. Indeed, different tree structures, such as AVL, Red-Black, and B-Trees, have evolved to address various performance issues associated with node insertions, deletions, and traversals.

For simplicity, let’s consider a basic implementation in pseudocode:

1. If the tree is empty, insert new_node as the root node (obviously!)
2. while (tree is NOT empty):
  2a. If (current_node is empty), insert it here and stop;
  2b. Else if (new_node > current_node), try inserting to the right
      of this node (and repeat Step 2)
  2c. Else if (new_node < current_node), try inserting to the left
      of this node (and repeat Step 2)
  2d. Else value is already in the tree

In this naive implementation, a divide and conquer approach is assumed. Anything less than the current node value goes to the left, anything greater goes right, and duplicates are rejected. Notice how this strategy immediately lends itself to a recursive solution as a tree in this instance can also be a sub-tree.

<?php
class BinaryTree
{
...
    public function insert($item) {
        $node = new BinaryNode($item);
        if ($this->isEmpty()) {
            // special case if tree is empty
            $this->root = $node;
        }
        else {
            // insert the node somewhere in the tree starting at the root
            $this->insertNode($node, $this->root);
        }
    }
    protected function insertNode($node, &$subtree) {
        if ($subtree === null) {
            // insert node here if subtree is empty
            $subtree = $node;
        }
        else {
            if ($node->value > $subtree->value) {
                // keep trying to insert right
                $this->insertNode($node, $subtree->right);
            }
            else if ($node->value < $subtree->value) {
                // keep trying to insert left
                $this->insertNode($node, $subtree->left);
            }
            else {
                // reject duplicates
            }
        }
    }
}

Deleting nodes is a whole other story, which we’ll leave for another time as it will require a more in-depth treatment than this article allows.

Walking the Tree

Notice how we started at the root node and walked the tree, node-by-node, to find an empty node? There are 4 general strategies used to traverse a tree:

• pre-order – process the current node and then traverse the left and right sub-trees.
• in-order (symmetric) – traverse left first, process the current node, and then traverse right.
• post-order – traverse left and right first and then process the current node.
• level-order (breadth-first) – process the current node, then process all sibling nodes before traversing nodes on the next level.

The first three strategies are also known as a depth-first or depth-order search – in which one starts at the root (or an arbitrary node designated as the root) and traverses as far down a branch as possible, before backtracking. Each of these strategies are used in different operational contexts and situations, for example, pre-order traversal is suited to node insertions (as in our example) and sub-tree cloning (grafting). In-order traversal is commonly used for searching binary trees, while post-order is better suited for deleting (pruning) nodes.

To illustrate how an in-order traversal works, let’s make a few modifications to our example:

<?php
class BinaryNode
{
...
    // perform an in-order traversal of the current node
    public function dump() {
        if ($this->left !== null) {
            $this->left->dump();
        }
        var_dump($this->value);
        if ($this->right !== null) {
            $this->right->dump();
        }
    }
}
class BinaryTree
{
...
    public function traverse() {
        // dump the tree rooted at "root"
        $this->root->dump();
    }
}

Calling the traverse() method will display the entire tree in ascending order starting from the root node.

Conclusion

Well, here we are at the end already! In this article I introduced you to the tree data structure, and its simplest form – the binary tree. You’ve seen how nodes are inserted into the tree and how to recursively walk the tree in depth-order.

Next time I’ll discuss breadth-first search as well as introduce some new data structures. Stay tuned! Until then, I encourage you to explore other tree types and their respective algorithms for inserting and deleting nodes.

Image via Fotolia

Frequently Asked Questions (FAQs) about PHP Tree Data Structures