Key Takeaways
- Graphs are mathematical constructs used to model relationships between key/value pairs and have numerous real-world applications such as network optimization, traffic routing, and social network analysis. They are made up of vertices (nodes) and edges (lines) that connect them, which can be directed or undirected, and weighted or unweighted.
- Graphs can be represented in two ways: as an adjacency matrix or an adjacency list. Adjacency lists are more space-efficient, especially for sparse graphs where most pairs of vertices are unconnected, while adjacency matrices facilitate quicker lookups.
- A common application of graph theory is finding the least number of hops (i.e., the shortest path) between any two nodes. This can be achieved using breadth-first search, which involves traversing the graph level by level from a designated root node. This process requires maintaining a queue of unvisited nodes.
- Dijkstra’s algorithm is widely used to find the shortest or most optimal path between any two nodes in a graph. This involves examining each edge between all possible pairs of vertices, starting from the source node, and maintaining an updated set of vertices with the shortest total distance until the target node is reached.
In one of my previous articles I introduced you to the tree data structure. Now I’d like to explore a related structure – the graph. Graphs have a number of real-world applications, such as network optimization, traffic routing, and social network analysis. Google’s PageRank, Facebook’s Graph Search, and Amazon’s and NetFlix’s recommendations are some examples of graph-driven applications.
In this article I’ll explore two common problems in which graphs are used – the Least Number of Hops and Shortest-Path problems.
A graph is a mathematical construct used to model the relationships between key/value pairs. A graph comprises a set of vertices (nodes) and an arbitrary number of edges (lines) which connect them. These edges can be directed or undirected. A directed edge is simply an edge between two vertices, and edge A→B is not considered the same as B→A. An undirected edge has no orientation or direction; edge A-B is equivalent to B-A. A tree structure which we learned about last time can be considered a type of undirected graph, where each vertex is connected to at least one other vertex by a simple path.
Graphs can also be weighted or unweighted. A weighted graph, or a network, is one in which a weight or cost value is assigned to each of its edges. Weighted graphs are commonly used in determining the most optimal path, most expedient, or the lowest “cost” path between two points. GoogleMap’s driving directions is an example that uses weighted graphs.
The Least Number of Hops
A common application of graph theory is finding the least number of hops between any two nodes. As with trees, graphs can be traversed in one of two ways: depth-first or breadth-first. We covered depth-first search in the previous article, so let’s take a look at breadth-first search.
Consider the following graph:
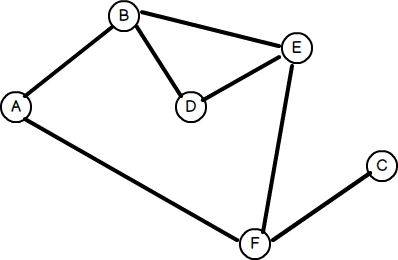
For the sake of simplicity, let’s assume that the graph is undirected – that is, the edges in any direction are identical. Our task is to find the least number of hops between any two nodes.
In a breadth-first search, we start at the root node (or any node designated as the root), and work our way down the tree level by level. In order to do that, we need a queue to maintain a list of unvisited nodes so that we can backtrack and process them after each level.
The general algorithm looks like this:
1. Create a queue 2. Enqueue the root node and mark it as visited 3. While the queue is not empty do: 3a. dequeue the current node 3b. if the current node is the one we're looking for then stop 3c. else enqueue each unvisited adjacent node and mark as visited
But how do we know which nodes are adjacent, let alone unvisited, without traversing the graph first? This brings us to the problem of how a graph data structure can be modelled.
Representing the Graph
There are generally two ways to represent a graph: either as an adjacency matrix or an adjacency list. The above graph represented as an adjacency list looks like this:
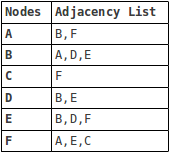
Represented as a matrix, the graph looks like this, where 1 indicates an “incidence” of an edge between 2 vertices:
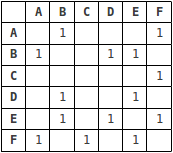
Adjacency lists are more space-efficient, particularly for sparse graphs in which most pairs of vertices are unconnected, while adjacency matrices facilitate quicker lookups. Ultimately, the choice of representation will depend on what type of graph operations are likely to be required.
Let’s use an adjacency list to represent the graph:
<?php
$graph = array(
'A' => array('B', 'F'),
'B' => array('A', 'D', 'E'),
'C' => array('F'),
'D' => array('B', 'E'),
'E' => array('B', 'D', 'F'),
'F' => array('A', 'E', 'C'),
);And now, let’s see what the general breadth-first search algorithm’s implementation looks like:
<?php
class Graph
{
protected $graph;
protected $visited = array();
public function __construct($graph) {
$this->graph = $graph;
}
// find least number of hops (edges) between 2 nodes
// (vertices)
public function breadthFirstSearch($origin, $destination) {
// mark all nodes as unvisited
foreach ($this->graph as $vertex => $adj) {
$this->visited[$vertex] = false;
}
// create an empty queue
$q = new SplQueue();
// enqueue the origin vertex and mark as visited
$q->enqueue($origin);
$this->visited[$origin] = true;
// this is used to track the path back from each node
$path = array();
$path[$origin] = new SplDoublyLinkedList();
$path[$origin]->setIteratorMode(
SplDoublyLinkedList::IT_MODE_FIFO|SplDoublyLinkedList::IT_MODE_KEEP
);
$path[$origin]->push($origin);
$found = false;
// while queue is not empty and destination not found
while (!$q->isEmpty() && $q->bottom() != $destination) {
$t = $q->dequeue();
if (!empty($this->graph[$t])) {
// for each adjacent neighbor
foreach ($this->graph[$t] as $vertex) {
if (!$this->visited[$vertex]) {
// if not yet visited, enqueue vertex and mark
// as visited
$q->enqueue($vertex);
$this->visited[$vertex] = true;
// add vertex to current path
$path[$vertex] = clone $path[$t];
$path[$vertex]->push($vertex);
}
}
}
}
if (isset($path[$destination])) {
echo "$origin to $destination in ",
count($path[$destination]) - 1,
" hopsn";
$sep = '';
foreach ($path[$destination] as $vertex) {
echo $sep, $vertex;
$sep = '->';
}
echo "n";
}
else {
echo "No route from $origin to $destinationn";
}
}
}
Running the following examples, we get:
<?php
$g = new Graph($graph);
// least number of hops between D and C
$g->breadthFirstSearch('D', 'C');
// outputs:
// D to C in 3 hops
// D->E->F->C
// least number of hops between B and F
$g->breadthFirstSearch('B', 'F');
// outputs:
// B to F in 2 hops
// B->A->F
// least number of hops between A and C
$g->breadthFirstSearch('A', 'C');
// outputs:
// A to C in 2 hops
// A->F->C
// least number of hops between A and G
$g->breadthFirstSearch('A', 'G');
// outputs:
// No route from A to G
If we had used a stack instead of a queue, the traversal becomes a depth-first search.
Finding the Shortest-Path
Another common problem is finding the most optimal path between any two nodes. Earlier I mentioned GoogleMap’s driving directions as an example of this. Other applications include planning travel itineraries, road traffic management, and train/bus scheduling.
One of the most famous algorithms to address this problem was invented in 1959 by a 29 year-old computer scientist by the name of Edsger W. Dijkstra. In general terms, Dijkstra’s solution involves examining each edge between all possible pairs of vertices starting from the source node and maintaining an updated set of vertices with the shortest total distance until the target node is reached, or not reached, whichever the case may be.
There are several ways to implement the solution, and indeed, over years following 1959 many enhancements – using MinHeaps, PriorityQueues, and Fibonacci Heaps – were made to Dijkstra’s original algorithm. Some improved performance, while others were designed to address shortcomings in Dijkstra’s solution since it only worked with positive weighted graphs (where the weights are positive values).
Here’s an example of a (positive) weighted graph:
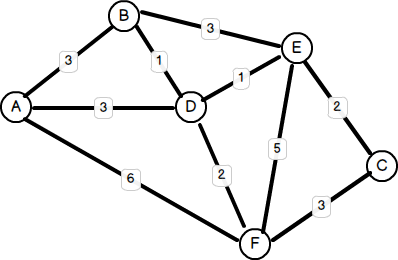
We can represent this graph as an adjacency list, as follows:
<?php
$graph = array(
'A' => array('B' => 3, 'D' => 3, 'F' => 6),
'B' => array('A' => 3, 'D' => 1, 'E' => 3),
'C' => array('E' => 2, 'F' => 3),
'D' => array('A' => 3, 'B' => 1, 'E' => 1, 'F' => 2),
'E' => array('B' => 3, 'C' => 2, 'D' => 1, 'F' => 5),
'F' => array('A' => 6, 'C' => 3, 'D' => 2, 'E' => 5),
);And here’s an implementation using a PriorityQueue to maintain a list of all “unoptimized” vertices:
<?php
class Dijkstra
{
protected $graph;
public function __construct($graph) {
$this->graph = $graph;
}
public function shortestPath($source, $target) {
// array of best estimates of shortest path to each
// vertex
$d = array();
// array of predecessors for each vertex
$pi = array();
// queue of all unoptimized vertices
$Q = new SplPriorityQueue();
foreach ($this->graph as $v => $adj) {
$d[$v] = INF; // set initial distance to "infinity"
$pi[$v] = null; // no known predecessors yet
foreach ($adj as $w => $cost) {
// use the edge cost as the priority
$Q->insert($w, $cost);
}
}
// initial distance at source is 0
$d[$source] = 0;
while (!$Q->isEmpty()) {
// extract min cost
$u = $Q->extract();
if (!empty($this->graph[$u])) {
// "relax" each adjacent vertex
foreach ($this->graph[$u] as $v => $cost) {
// alternate route length to adjacent neighbor
$alt = $d[$u] + $cost;
// if alternate route is shorter
if ($alt < $d[$v]) {
$d[$v] = $alt; // update minimum length to vertex
$pi[$v] = $u; // add neighbor to predecessors
// for vertex
}
}
}
}
// we can now find the shortest path using reverse
// iteration
$S = new SplStack(); // shortest path with a stack
$u = $target;
$dist = 0;
// traverse from target to source
while (isset($pi[$u]) && $pi[$u]) {
$S->push($u);
$dist += $this->graph[$u][$pi[$u]]; // add distance to predecessor
$u = $pi[$u];
}
// stack will be empty if there is no route back
if ($S->isEmpty()) {
echo "No route from $source to $targetn";
}
else {
// add the source node and print the path in reverse
// (LIFO) order
$S->push($source);
echo "$dist:";
$sep = '';
foreach ($S as $v) {
echo $sep, $v;
$sep = '->';
}
echo "n";
}
}
}
As you can see, Dijkstra’s solution is simply a variation of the breadth-first search!
Running the following examples yields the following results:
<?php
$g = new Dijkstra($graph);
$g->shortestPath('D', 'C'); // 3:D->E->C
$g->shortestPath('C', 'A'); // 6:C->E->D->A
$g->shortestPath('B', 'F'); // 3:B->D->F
$g->shortestPath('F', 'A'); // 5:F->D->A
$g->shortestPath('A', 'G'); // No route from A to G
Summary
In this article I’ve introduced the basics of graph theory, two ways of representing graphs, and two fundamental problems in the application of graph theory. I’ve shown you how a breadth-first search is used to find the least number of hops between any two nodes, and how Dijkstra’s solution is used to find the shortest-path between any two nodes.
Image via Fotolia
Frequently Asked Questions (FAQs) about Graphs in Data Structures
What is the difference between a graph and a tree in data structures?
A graph and a tree are both non-linear data structures, but they have some key differences. A tree is a type of graph, but not all graphs are trees. A tree is a connected graph without any cycles. It has a hierarchical structure with a root node and child nodes. Each node in a tree has a unique path from the root. On the other hand, a graph can have cycles and its structure is more complex. It can be connected or disconnected and nodes can have multiple paths between them.
How are graphs represented in data structures?
Graphs in data structures can be represented in two ways: adjacency matrix and adjacency list. An adjacency matrix is a 2D array of size V x V where V is the number of vertices in the graph. If there is an edge between vertices i and j, then the cell at the intersection of row i and column j will be 1, otherwise 0. An adjacency list is an array of linked lists. The index of the array represents a vertex and each element in its linked list represents the other vertices that form an edge with the vertex.
What are the types of graphs in data structures?
There are several types of graphs in data structures. A simple graph is a graph with no loops and no more than one edge between any two vertices. A multigraph can have multiple edges between vertices. A complete graph is a simple graph where every pair of vertices is connected by an edge. A weighted graph assigns a weight to each edge. A directed graph (or digraph) has edges with a direction. The edges point from one vertex to another.
What are the applications of graphs in computer science?
Graphs are used in numerous applications in computer science. They are used in social networks to represent connections between people. They are used in web crawling to visit web pages and build a search index. They are used in network routing algorithms to find the best path between two nodes. They are used in biology to model and analyze biological networks. They are also used in computer graphics and physics simulations.
What are the graph traversal algorithms?
There are two main graph traversal algorithms: Depth-First Search (DFS) and Breadth-First Search (BFS). DFS explores as far as possible along each branch before backtracking. It uses a stack data structure. BFS explores all the vertices at the present depth before going to the next level. It uses a queue data structure.
How to implement a graph in Java?
In Java, a graph can be implemented using a HashMap to store the adjacency list. Each key in the HashMap is a vertex and its value is a LinkedList containing the vertices that it is connected to.
What is a bipartite graph?
A bipartite graph is a graph whose vertices can be divided into two disjoint sets such that every edge connects a vertex in one set to a vertex in the other set. No edge connects vertices within the same set.
What is a subgraph?
A subgraph is a graph that is a part of another graph. It has some (or all) vertices of the original graph and some (or all) edges of the original graph.
What is a cycle in a graph?
A cycle in a graph is a path that starts and ends at the same vertex and has at least one edge.
What is a path in a graph?
A path in a graph is a sequence of vertices where each pair of consecutive vertices is connected by an edge.