Data Structures for PHP Devs: Heaps

In past couple articles I’ve introduced you to three basic data structures: stack, queue, and tree. In this article I’ll introduce you to another abstract data type that is closely related: heap. Heaps are specialized tree-like data structures which satisfy the heap property – the node value (key) of any parent is always ordered with respect to its child node values across the entire tree. Let’s take a closer look!

Key Takeaways

• Heaps are specialized tree-like data structures where the node value of any parent is always ordered with respect to its child node values across the entire tree. There are several heap variants including maxheap, minheap and a specialized data type called a Priority Queue.
• Heaps are usually implemented as complete binary trees, but unlike binary trees, there is no implied ordering of siblings and cousins, nor is there any implied sequence for an in-order traversal. They have operations like create, isEmpty, insert, and extract.
• Implementing a heap as an array is possible. A binary node has at most two children, therefore for any n number of nodes a binary heap will have at most 2n + 1 nodes. The insertion strategy is the exact opposite of extraction.
• PHP provides classes like SplHeap, SplMaxHeap, SplMinHeap and SplPriorityQueue to handle heaps. The Priority Queue is a specialized abstract data type that behaves like a queue, but is usually implemented as a heap. It has many real-world applications, such as service desks/ticket escalation and improving the performance of certain graph applications.

Heaps

There are several heap variants. For instance, if parent keys are ordered such that they are of equal or greater value than their children, and the highest key is at the root, the heap is said to be a maxheap. If parent keys are ordered such that they are of equal or lower value than their children, with the lowest key at the root, the heap is called a minheap. SPL (PHP>=5.3.0) provides a basic heap, minheap, maxheap, and a specialized data type called a Priority Queue.

So here’s an example of what a heap looks like:

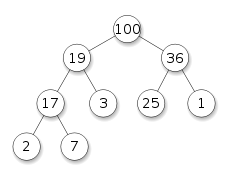
The figure above depicts a complete binary maxheap. It’s binary because each node has exactly two children, and a maxheap because the highest value key is at the root node and all parent nodes have values greater than their children.

While heaps are usually implemented as complete binary trees, unlike binary trees there is no implied ordering of siblings and cousins, nor is there any implied sequence for an in-order traversal.

Heaps are a variant of the table data type so they also have the same basic operations:

• create – create an empty heap.
• isEmpty – determine if the heap is empty.
• insert – add an item to the heap.
• extract – remove the topmost item (root) item from the heap.

Unlike a table, the retrieve and delete operations for a heap are combined into a single extract operation, so let’s focus on how the extract operation works first.

The condition for removing an item from the heap is that we can only remove the root node. Let’s say we removed the root node (100) from the above example. We would be left with two disjoint heaps. We need a method of transforming the remaining nodes back into a single heap after the root is removed. Joining them is easily accomplished by moving the last node to the root, but we’re left with a resulting structure that fails the heap property. Such a structure is called a semiheap.

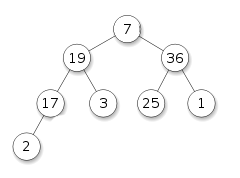
We now need a way to transform the semiheap into a heap. One strategy is to trickle the root item down the tree until it reaches a node where it will not be out of place. We iteratively compare the value of the root node to its children and swap places with the larger child until it arrives at a node where no child has a greater (or equal) value than itself.

Implementing a Heap as an Array

We can naively implement a binary maxheap as an array. A binary bode has at most two children, therefore for any n number of nodes a binary heap will have at most 2n + 1 nodes.

Here’s what an implementation looks like:

<?php
class BinaryHeap
{
    protected $heap;
    public function __construct() {
        $this->heap  = array();
    }
    public function isEmpty() {
        return empty($this->heap);
    }
    public function count() {
        // returns the heapsize
        return count($this->heap) - 1;
    }
    public function extract() {
        if ($this->isEmpty()) {
            throw new RunTimeException('Heap is empty');
        }
        // extract the root item
        $root = array_shift($this->heap);
        if (!$this->isEmpty()) {
            // move last item into the root so the heap is
            // no longer disjointed
            $last = array_pop($this->heap);
            array_unshift($this->heap, $last);
            // transform semiheap to heap
            $this->adjust(0);
        }
        return $root;
    }
    public function compare($item1, $item2) {
        if ($item1 === $item2) {
            return 0;
        }
        // reverse the comparison to change to a MinHeap!
        return ($item1 > $item2 ? 1 : -1);
    }
    protected function isLeaf($node) {
        // there will always be 2n + 1 nodes in the
        // sub-heap
        return ((2 * $node) + 1) > $this->count();
    }
    protected function adjust($root) {
        // we've gone as far as we can down the tree if
        // root is a leaf
        if (!$this->isLeaf($root)) {
            $left  = (2 * $root) + 1; // left child
            $right = (2 * $root) + 2; // right child
            // if root is less than either of its children
            $h = $this->heap;
            if (
              (isset($h[$left]) &&
                $this->compare($h[$root], $h[$left]) < 0)
              || (isset($h[$right]) &&
                $this->compare($h[$root], $h[$right]) < 0)
            ) {
                // find the larger child
                if (isset($h[$left]) && isset($h[$right])) {
                  $j = ($this->compare($h[$left], $h[$right]) >= 0)
                      ? $left : $right;
                }
                else if (isset($h[$left])) {
                  $j = $left; // left child only
                }
                else {
                  $j = $right; // right child only
                }
                // swap places with root
                list($this->heap[$root], $this->heap[$j]) =
                  array($this->heap[$j], $this->heap[$root]);
                // recursively adjust semiheap rooted at new
                // node j
                $this->adjust($j);
            }
        }
    }
}

The insertion strategy is the exact opposite of extraction: we insert the item at the bottom of the heap and trickle it up to its correct location. Since we know that a complete binary tree with a full last level contains n/2 + 1 nodes, we can traverse the heap using a simple binary search.

public function insert($item) {
    // insert new items at the bottom of the heap
    $this->heap[] = $item;
    // trickle up to the correct location
    $place = $this->count();
    $parent = floor($place / 2);
    // while not at root and greater than parent
    while (
      $place > 0 && $this->compare(
        $this->heap[$place], $this->heap[$parent]) >= 0
    ) {
        // swap places
        list($this->heap[$place], $this->heap[$parent]) =
            array($this->heap[$parent], $this->heap[$place]);
        $place = $parent;
        $parent = floor($place / 2);
    }
}

So let’s see what happens when we insert a few items into the structure:

<?php
$heap = new BinaryHeap();
$heap->insert(19);
$heap->insert(36);
$heap->insert(54);
$heap->insert(100);
$heap->insert(17);
$heap->insert(3);
$heap->insert(25);
$heap->insert(1);
$heap->insert(67);
$heap->insert(2);
$heap->insert(7);

If you dump the heap structure you’ll notice that the items aren’t in any particular order. In fact, it’s not even in the order we would expect:

Array
(
    [0] => 100
    [1] => 67
    [2] => 54
    [3] => 36
    [4] => 19
    [5] => 7
    [6] => 25
    [7] => 1
    [8] => 17
    [9] => 2
    [10] => 3
)

However, if you extract the items, this is what you would get:

<?php
while (!$heap->isEmpty()) {
    echo $heap->extract() . "n";
}

100
67
54
36
25
19
17
7
3
2
1

SplMaxHeap and SplMinHeap

Fortunately for us, SplHeap, SplMaxHeap and SplMinHeap abstracts all of this for us. All we have to do is extend the base class and override the comparison method like so:

<?php
class MyHeap extends SplMaxHeap
{
    public function compare($item1, $item2) {
        return (int) $item1 - $item2;
    }
}

The compare method can perform any arbitrary comparison, as long as it returns – in the case of a SplMaxHeap – a positive integer if $item1 is greater than $item2, 0 if they are equal, or a negative integer otherwise. If extending SplMinHeap, it should instead return a positive integer if $item1 is less than $item2.

It’s not recommended to have multiple elements with the same value in a heap as they may end up in an arbitrary relative position.

SplPriorityQueue

The Priority Queue is a specialized abstract data type that behaves like a queue, but is usually implemented as a heap – in the case of SplPriorityQueue, as a maxheap. Prioritized queues have many real-world applications, such as service desks/ticket escalation. They are also essential in improving the performance of certain graph applications.

Like the SplHeap, you only have to override the base class and comparator method:

<?php
class PriQueue extends SplPriorityQueue
{
    public function compare($p1, $p2) {
        if ($p1 === $p2) return 0;
        // in ascending order of priority, a lower value
        // means higher priority
        return ($p1 < $p2) ? 1 : -1;
   }
}

The main difference in a SplPriorityQueue is that the insert operation expects a priority value – which can be a mixed data type. The insert operation uses the priority to sift the element up the heap based on the returned result of your comparator.

For illustration purposes, let’s use integer priorities:

<?php
$pq = new PriQueue();
$pq->insert('A', 4);
$pq->insert('B', 3);
$pq->insert('C', 5);
$pq->insert('D', 8);
$pq->insert('E', 2);
$pq->insert('F', 7);
$pq->insert('G', 1);
$pq->insert('H', 6);
$pq->insert('I', 0);
while ($pq->valid()) {
    print_r($pq->current());
    echo "n";
    $pq->next();
}

I
G
E
B
A
C
H
F
D 

Notice that our items are displayed in order of priority – highest to lowest (the lower the value, the higher the priority). You can reverse the priority order by changing the comparator to return a positive integer if $p1 is greater than $p2.

By default, only the element’s data is extracted. If you wanted to extract the priority values only, or both the data and priority, you can set the extract flag like this:

<?php
// extract just the priority
$pq->setExtractFlags(SplPriorityQueue::EXTR_PRIORITY);
// extract both data and priority (returns an associative
// array for each element)
$pq->setExtractFlags(SplPriorityQueue::EXTR_BOTH);

Summary

I’ve introduced you to the heap abstract data type and showed you how items are inserted and extracted from a heap using a simple array implementation. We’ve also seen how the comparator is used in min and maxheaps, and how the Priority Queue operates. Stay tuned; in the next article I’ll discuss graphs!

Image via Fotolia

Frequently Asked Questions about Heap Data Structures in PHP