Vector Graphics in Sass

Sass is a very powerful tool and many of us are still examining it’s limits. What can we do with it and how far can we push it?

After throwing ideas at Hugo Giraudel, I got myself very excited about one idea; a 2D graphics engine. This may be confusing, because CSS and thus Sass is already part of the realm of graphics. Instead of styling content, I wanted to (ab)use Sass to render an image, pixel by pixel. The output can be drawn as a box-shadow value on a 1×1 pixel element.

Examining strategies

One way is to iterate through a grid and a list of objects, and check if a pixel should be drawn. Sass would have to process n x width x height iterations, where n is the amount of objects. That is a lot of work so not very performant, especially considering loops in Sass aren’t fast. Instead of rendering the entire grid, it is possible to render only parts that may contain an object by getting a so called bounding box. Check out the demo.

A better option is to use paths.

Paths may sound familiar to you. It is a common term in graphics software like Adobe Illustrator and Adobe Photoshop, but the term occurs in web technologies like SVG and HTML5 too. A path is a list of coordinates that are connected in sequence. All I need to define a shape is a couple of coordinates. If you are familiar with paths, you probably know you can make curved paths as well. For now, I will stick to straight lines.

The process of converting a vector path to pixels – or in our case a vector path to a box-shadow – is called rasterizing.

Scanline algorithm

Paths are often rendered using the scanline algorithm. Personally, whenever I hear the word “algorithm” I panic and execute whatever exit strategy I have at hand. This algorithm however is surprisingly comprehensible, so don’t be scared just yet!

We iterate through the vertical pixels. For every row, we store the intersections of all lines of that path. After iterating through all lines, we sort and iterate through the intersections from left to right. At every intersection, we toggle drawing.

Sass implementation

Before rendering anything, it is useful to know what to render. We have to define a path. I think a list of coordinates is a pretty good set-up:

$square: (
  (0, 0), (64, 0),
  (64, 64), (0, 64)
);

These can easily be scaled and translated (moved):

@function scale($path, $scale) {
  @for $n from 1 through length($path) {
    $coords: nth($path, $n);

    $path: set-nth($path, $n, (
      nth($coords, 1) * $scale,
      nth($coords, 2) * $scale
    ));
  }

  @return $path;
}

@function translate($path, $x, $y) {
  @for $n from 1 through length($path) {
    $coords: nth($path, $n);

    $path: set-nth($path, $n, (
      nth($coords, 1) + $x,
      nth($coords, 2) + $y
    ));
  }

  @return $path;
}

To render a specific color, we may want to pass a color to the function that will output a list of box-shadows, like so:

$shadows: ();

// Append more shadows
$shadows: render($shadows, $square, #f00);

In our render() function, we have to list new shadows and return them. This is the outline of render():

@function render($list, $path, $color) {
  // List to store shadows
  $shadows: ();

  // Do a lot of thinking

  @if length($shadows) > 0 {
    @return append($list, $shadows, comma);
  }

  @return $shadows;
}

To calculate the area we have to draw, we can iterate through all coordinates in the path, and store the minimum and maximum value on the y-axis. This way we know where to start and stop drawing on the y-axis. Knowing what to render on the x-axis will be calculated using the lines of the path, which will be covered shortly.

// Initial values
$top: null;
$bottom: null;

@each $coord in $path {
    $y: nth($coord, 2);

    // @if $top is still null, let's set current value
    // @else get the smaller value between previous y and current y
    @if $top == null { $top: $y; }
    @else { $top: min($y, $top); }

    // Same thing for the bottom, but get the largest value instead
    @if $bottom == null { $bottom: $y; }
    @else { $bottom: max($y, $bottom); }
}

Knowing the vertical boundary of a path, we can iterate through the rows, and use this to calculate intersections of the lines of the path. The intersections are then sorted to make sure the drawing is done right. We will go over the drawing logic later.

// If there is something to draw at all
@if $bottom - $top > 0 {
  // Iterate through rows
  @for $y from $top through $bottom {
    // Get intersections
    $intersections: intersections($path, $y);

    @if type-of($intersections) == 'list' and length($intersections) > 0 {
        $intersections: quick-sort($intersections, 'compare');

        // Drawing logic
      }
    }
  }
}

The function intersections($path, $y) is the function used to get the intersections of a path at a specific y coordinate. The outline is fairly simple. We iterate through the path, and for every line we search intersections. Finally, we return a list of those intersections.

@function intersections($path, $y) {
  $intersections: ();
  $length: length($path);

  // Iterate through path
  @for $n from 1 through $length {
    // Intersection algorithm here
  }

  @return $intersections;
}

Time for a Sass-pause. Getting the intersection of a line is tricky. By getting the height of the line (b_y – a_y), we can determine the progress of y over the height (y – a_y / height). This should be a number between or equal to 0 and 1. If not, y does not intersect with the line at all.

Because the lines are linear, we can multiply this number with the line’s width (b_x – a_x), so we get the x coordinate relative of the line’s position. All that is left is add the horizontal position of the line (… + a_x), and we have our final x coordinate!

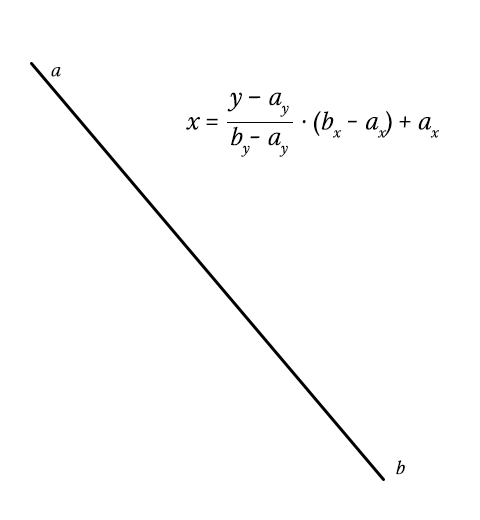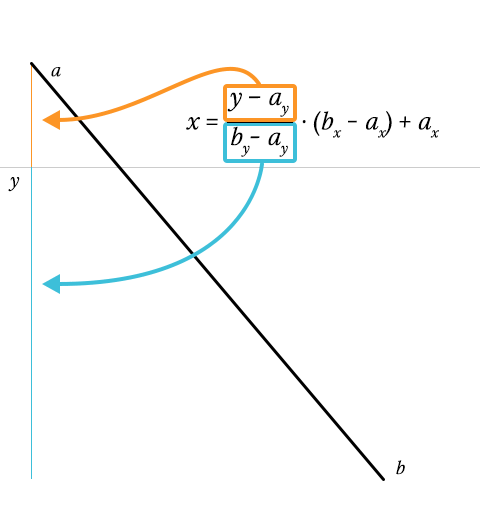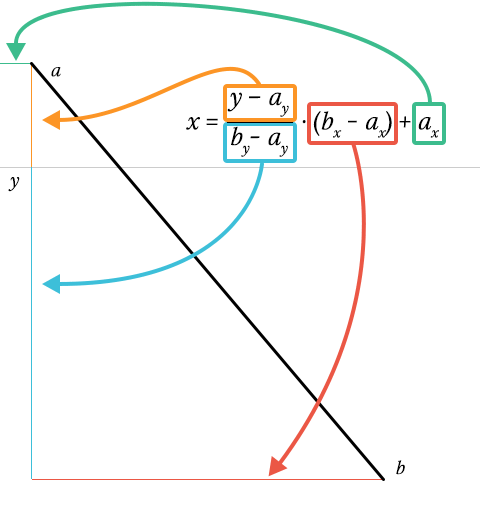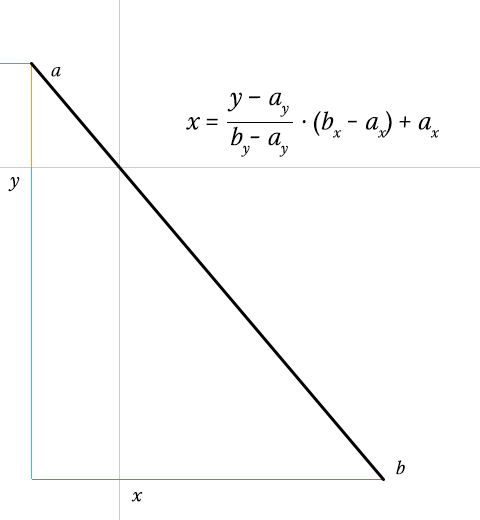
Back to Sass. Let’s implement the above:

// Get current and next point in this path, which makes a line
$a: nth($path, $n);
$b: nth($path, ($n % $length) + 1);

// Get boundaries of this line
$top: min(nth($a, 2), nth($b, 2));
$bottom: max(nth($a, 2), nth($b, 2));

// Get size of the line
$height: nth($b, 2) - nth($a, 2);
$width: nth($b, 1) - nth($a, 1);

// Is line within boundaries?
@if $y >= $top and $y <= $bottom and $height != 0 {
  // Get intersection at $y and add it to the list
  $x: ($y - nth($a, 2)) / $height * $width + nth($a, 1);
  $intersections: append($intersections, $x);
}

As for the drawing logic, we can look at the first animation that demonstrates the scanline algorithm. As you can see, it draws intersection 1 to 2, 3 to 4, etc.

For every intersection, we toggle drawing. Then, we simply fill the pixels into $shadows.

// Boolean to decide whether to draw or not
$draw: false;

// Iterate through intersections
@for $n from 1 through length($intersections) {
  // To draw or not to draw?
  $draw: not $draw;

  // Should we draw?
  @if $draw {
    // Get current and next intersection
    $current: nth($intersections, $n);
    $next: nth($intersections, $n + 1);

    // Get x coordinates of our intersections
    $from: round($current);
    $to: round($next);

    // Draw the line between the x coordinates
    @for $x from $from through $to {
      $value: ($x + 0px) ($y + 0px) $color;
      $shadows: append($shadows, $value, comma);
    }
  }
}

Conclusion

Let’s glimpse back at what the hell just happened:

1. Define a path
2. Create bounding box of path
3. Iterate over y-axis of bounding box
4. Get intersections of all lines within a path
5. Sort intersections by x coordinate
6. Iterate through intersections
7. For every odd intersection, draw until the next
8. Output magic

See the demo (and complete code)

So, is any of this useful? Not remotely. Performance is really, really bad. Drawing some basic objects takes several minutes to render. LibSass however makes it less painful, perhaps even bearable. But who are we kidding, right? If you intend to render vector paths, stick to SVG or the Canvas element or even WebGL. All of these do the rasterizing for you, and you get much more options and way better performance.

What this does prove however, is that Sass is pretty powerful, and we can do crazy funky things with it. Any application that can be written in Sass, will eventually be written in Sass.

Frequently Asked Questions about Vector Graphics with SASS