An Introduction to Genetic Algorithms
A genetic algorithm is a procedure that searches for the best solution to a problem using operations that emulate the natural processes involved in evolution, such as “survival of the fittest”, chromosomal crossover, and mutation. This article provides a gentle introduction to writing genetic algorithms, discusses some important considerations when writing your own algorithm, and presents a few examples of genetic algorithms in action.
Key Takeaways
- Genetic algorithms simulate evolutionary processes like “survival of the fittest” to find optimal solutions to complex problems, utilizing mechanisms such as selection, crossover, and mutation.
- In genetic algorithms, potential solutions are represented as chromosomes, and their suitability is evaluated using a fitness function, which determines their probability of being selected for reproduction.
- The process of crossover combines features from pairs of parent solutions to create new offspring, while mutation introduces random changes to offspring, preserving genetic diversity and potentially uncovering new solutions.
- Genetic algorithms are effective for problems where traditional search and optimization methods falter, due to their ability to explore large, complex solution spaces efficiently.
- Practical applications of genetic algorithms range from designing antennas with enhanced performance characteristics to optimizing web designs, illustrating their versatility and power in solving real-world problems.
Guessing the Unknown
The year is 2369 and humankind has spread out across the stars. You’re a young, bright doctor stationed at a star base in deep space that’s bustling with interstellar travelers, traders, and the occasional ne’er-do-well. Almost immediately after your arrival, one of the station’s shopkeeps takes an interest in you. He claims to be nothing more than a simple tailor, but rumors say he’s black ops working for a particularly nasty regime.
The two of you begin to enjoy weekly lunches together and discuss everything from politics to poetry. Even after several months, you still aren’t certain whether he’s making romantic gestures or fishing for secrets (not that you know any). Perhaps it’s a bit of both.
One day over lunch he presents you with this challenge: “I have a message for you, dear doctor! I can’t say what it is, of course. But I will tell you it’s 12 characters long. Those characters can be any letter of the alphabet, a space, or punctuation mark. And I’ll tell you how far off your guesses are. You’re smart; do you think you can figure it out?”
You return to your office in the medical bay still thinking about what he said. Suddenly, a gene sequencing simulation you left running on a nearby computer as part of an experiment gives you an idea. You’re not a code breaker, but maybe you can leverage your expertise in genetics to figure out his message!
A Bit of Theory
As I mentioned at the beginning, a genetic algorithm is a procedure that searches for a solution using operations that emulate processes that drive evolution. Over many iterations, the algorithm selects the best candidates (guesses) from a set of possible solutions, recombines them, and checks which combinations moved it closer to a solution. Less beneficial candidates are discarded.
In the scenario above, any character in the secret message can be A–Z, a space, or a basic punctuation mark. Let’s say that gives us the following 32-character “alphabet” to work with: ABCDEFGHIJKLMNOPQRSTUVWXYZ -.,!? This means there are 3212 (roughly 1.15×1018) possible messages, but only one of those possibilities is the correct one. It would take too long to check each possibility. Instead, a genetic algorithm will randomly select 12 characters and ask the tailor/spy to score how close the result is to his message. This is more efficient than a brute-force search, in that the score lets us fine-tune future candidates. The feedback gives us the ability to gauge the fitness of each guess and hopefully avoid wasting time on the dead-ends.
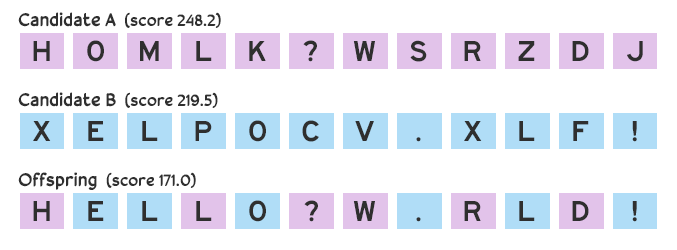
Suppose we make three guesses: HOMLK?WSRZDJ, BGK KA!QTPXC, and XELPOCV.XLF!. The first candidate receives a score of 248.2, the second receives 632.5, and the third receives 219.5. How the score is calculated depends on the situation, which we’ll discuss later, but for now let’s assume it’s based on deviation between the candidate and target message: a perfect score is 0 (that is, there are no deviations; the candidate and the target are the same), and a larger score means there’s a greater deviation. The guesses that scored 248.2 and 219.5 are closer to what the secret message might be than the guess that scored 635.5.
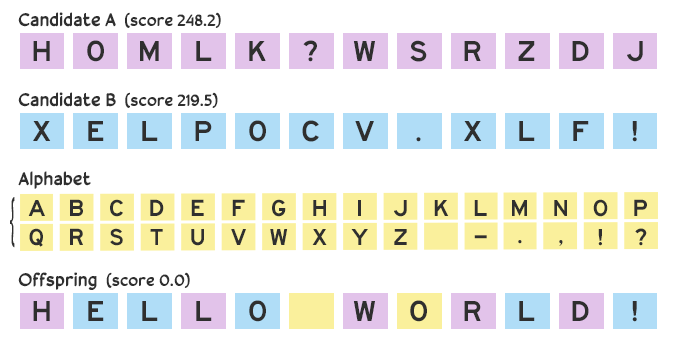
Future guesses are made by combining the best attempts. There are many ways to combine candidates, but for now we’ll consider a simple crossover method: each character in the new guess has a 50–50 chance of being copied from the first or second parent candidate. If we take the two guesses HOMLK?WSRZDJ and XELPOCV.XLF!, the first character of our offspring candidate has a 50% chance of being H and 50% chance of being X, the second character will be either O or E, and so on. The offspring could be HELLO?W.RLD!.
However, a problem can arise over multiple iterations if we only use values from the parent candidates: a lack of diversity. If we have one candidate consisting of all A’s and another of all B’s, then any offspring generated with them solely by crossover would consist only of A’s and B’s. We’re out of luck if the solution contains a C.
To mitigate this risk and maintain diversity while still narrowing in on a solution, we can introduce minor changes. Rather than a straight 50–50 split, we afford a small chance that an arbitrary value from the alphabet is picked instead. With this mutation the offspring might become HELLO WORLD!.
Unsurprisingly, genetic algorithms borrow a lot of vocabulary from genetic science. So before we go much further, let’s refine some of our terminology:
-
Allele: a member of the genetic alphabet. How alleles are defined depends on the algorithm. For example,
0and1might be alleles for a genetic algorithm working with binary data, an algorithm working with code might use function pointers, etc. In our secret message scenario, the alleles were the letters of the alphabet, space, and various punctuation. -
Chromosome: a given sequence of alleles; a candidate solution; a “guess”. In our scenario,
HOMLK?WSRZDJ,XELPOCV.XLF!, andHELLO WORLD!are all chromosomes. -
Gene: the allele at a specific location in the chromosome. For the chromosome
HOMLK?WSRZDJ, the first gene isH, the second gene isO, the third isM, and so on. -
Population: a collection of one or more candidate chromosomes proposed as a solution to the problem.
-
Generation: the population during a specific iteration of the algorithm. The candidates in one generation provide genes to produce the next generation’s population.
-
Fitness: a measure that evaluates a candidate’s closeness to the desired solution. Fitter chromosomes are more likely to pass their genes to future candidates while less fit chromosomes are more likely to be discarded.
-
Selection: the process of choosing some candidates to reproduce (used to create new candidate chromosomes) and discarding others. Multiple selection strategies exist, which vary in their tolerance for selecting weaker candidates.
-
Reproduction: the process of combining genes from one or more candidates to produce new candidates. The donor chromosomes are called parents, and the resulting chromosomes are called as offspring.
-
Mutation: the random introduction of aberrant genes in offspring to prevent the loss of genetic diversity over many generations.
Show Me Some Code!
I suspect that, given the high-level overview and list of terminology, you’re probably itching to see some code now. So, let’s look at some JavaScript that solves our secret message problem. As you read through, I invite you to think about which methods might be considered “boilerplate code” and which methods’ implementations more closely bound to the problem we’re trying to solve:
class Candidate {
constructor(chromosome, fitness) {
this.chromosome = chromosome;
this.fitness = fitness;
}
/**
* Convenience method to sort an array of Candidate
* objects.
*/
static sort(candidates, asc) {
candidates.sort((a, b) => (asc)
? (a.fitness - b.fitness)
: (b.fitness - a.fitness)
);
}
}
class GeneticAlgorithm {
constructor(params) {
this.alphabet = params.alphabet;
this.target = params.target;
this.chromosomeLength = params.target.length;
this.populationSize = params.populationSize;
this.selectionSize = params.selectionSize;
this.mutationRate = params.mutationRate;
this.mutateGeneCount = params.mutateGeneCount;
this.maxGenerations = params.maxGenerations;
}
/**
* Convenience method to return a random integer [0-max).
*/
randomInt(max) {
return Math.floor(Math.random() * max);
}
/**
* Create a new chromosome from random alleles.
*/
createChromosome() {
const chrom = [];
for (let i = 0; i < this.chromosomeLength; i++) {
chrom.push(this.alphabet[
this.randomInt(this.alphabet.length)
]);
}
return chrom;
}
/**
* Create the initial population with random chromosomes
* and assign each a fitness score for later evaluation.
*/
init() {
this.generation = 0;
this.population = [];
for (let i = 0; i < this.populationSize; i++) {
const chrom = this.createChromosome();
const score = this.calcFitness(chrom);
this.population.push(new Candidate(chrom, score));
}
}
/**
* Measure a chromosome’s fitness based on how close its
* genes match those of the target; uses mean squared
* error.
*/
calcFitness(chrom) {
let error = 0;
for (let i = 0; i < chrom.length; i++) {
error += Math.pow(
this.target[i].charCodeAt() - chrom[i].charCodeAt(),
2
);
}
return error / chrom.length;
}
/**
* Reduce the population to only the fittest candidates;
* elitist selection strategy.
*/
select() {
// lower MSE is better
Candidate.sort(this.population, true);
this.population.splice(this.selectionSize);
}
/**
* Apply crossover and mutation to create new offspring
* chromosomes and increase the population.
*/
reproduce() {
const offspring = [];
const numOffspring = this.populationSize /
this.population.length * 2;
for (let i = 0; i < this.population.length; i += 2) {
for (let j = 0; j < numOffspring; j++) {
let chrom = this.crossover(
this.population[i].chromosome,
this.population[i + 1].chromosome,
);
chrom = this.mutate(chrom);
const score = this.calcFitness(chrom);
offspring.push(new Candidate(chrom, score));
}
}
this.population = offspring;
}
/**
* Create a new chromosome through uniform crossover.
*/
crossover(chromA, chromB) {
const chromosome = [];
for (let i = 0; i < this.chromosomeLength; i++) {
chromosome.push(
this.randomInt(2) ? chromA[i] : chromB[i]
);
}
return chromosome;
}
/**
* (Possibly) introduce mutations to a chromosome.
*/
mutate(chrom) {
if (this.mutationRate < this.randomInt(1000) / 1000) {
return chrom;
}
for (let i = 0; i < this.mutateGeneCount; i++) {
chrom[this.randomInt(this.chromosomeLength)] =
this.alphabet[
this.randomInt(this.alphabet.length)
];
}
return chrom;
}
/**
* Return whether execution should continue processing
* the next generation or should stop.
*/
stop() {
if (this.generation > this.maxGenerations) {
return true;
}
for (let i = 0; i < this.population.length; i++) {
if (this.population[i].fitness == 0) {
return true;
}
}
return false;
}
/**
* Repeatedly perform genetic operations on the
* population of candidate chromosomes in an attempt to
* converge on the fittest solution.
*/
evolve() {
this.init();
do {
this.generation++;
this.select();
this.reproduce();
} while (!this.stop());
return {
generation: this.generation,
population: this.population
};
}
}
const result = new GeneticAlgorithm({
alphabet: Array.from('ABCDEFGHIJKLMNOPQRSTUVWXYZ !'),
target: Array.from('HELLO WORLD!'),
populationSize: 100,
selectionSize: 40,
mutationRate: 0.03,
mutateGeneCount: 2,
maxGenerations: 1000000
}).evolve();
console.log('Generation', result.generation);
Candidate.sort(result.population, true);
console.log('Fittest candidate', result.population[0]);
We begin by defining a Candidate data object simply to pair chromosomes with their fitness score. There’s also a static sorting method attached to it for the sake of convenience; it comes in handy when we need to find or output the fittest chromosomes.
Next we have a GeneticAlgorithm class that implements the genetic algorithm itself.
The constructor takes an object of various parameters needed for the simulation. It provides a way to specify a genetic alphabet, the target message, and other parameters that serve to define the constraints under which the simulation will run. In the example above, we’re expecting each generation to have a population of 100 candidates. From those, only 40 chromosomes will be selected for reproduction. We afford a 3% chance of introducing mutation and we’ll mutate up to two genes when it does occur. The maxGenerations value serves as a safeguard; if we don’t converge on a solution after one million generations, we’ll terminate the script regardless.
A point worth mentioning is the population, selection size, and maximum number of generations provided when running the algorithm are quite small. More complex problems may require a larger search space, which in turn increases the algorithm’s memory usage and the time it takes to run. However, small mutation parameters are strongly encouraged. If they become too large, we lose any benefit of reproducing candidates based on fitness and the simulation starts to become a random search.
Methods like randomInt(), init(), and run() can probably be considered boilerplate. But just because there’s boilerplate doesn’t mean it can’t have real implications for a simulation. For instance, genetic algorithms make heavy use of randomness. While the built-in Math.random() function is fine for our purposes, you require a more accurate random generator for other problems. Crypto.getRandomValues() provides more cryptographically strong random values.
Performance is also a consideration. I’m striving for legibility in this article, but keep in mind that operations will be repeated over and over again. You may find yourself needing to micro-optimize code within loops, use more memory-efficient data structures, and inline code rather than separating it into functions/methods, all regardless of your implementation language.
The implementation of the methods like calcFitness(), select(), reproduce(), and even stop() are specific to the problem we’re trying to solve.
calcFitness() returns a value measuring a chromosome’s fitness against some desired criteria — in our case, how close it matches the secret message. Calculating fitness is almost always situationally dependent; our implementation calculates the mean squared error using the ASCII values of each gene, but other metrics might be better suited. For example, I could have calculated the Hamming or Levenshtein distance between the two values, or even incorporated multiple measurements. Ultimately, it’s important for a fitness function to return a useful measurement with regard to the problem at hand, not simply a boolean “is-fit”/“isn’t-fit”.
The select() method demonstrates an elitist selection strategy — selecting only the fittest candidates across the entire population for reproduction. As I alluded to earlier, other strategies exist, such as tournament selection, which selects the fittest candidates from sets of individual candidates within the population, and Boltzmann selection, which applies increasing pressure to choose candidates. The purpose of these different approaches is to ensure chromosomes have an opportunity to pass on genes that may prove to be beneficial later, even though it may not be immediately apparent. In-depth descriptions of these and other selection strategies, as well as sample implementations, can easily be found online.

There are also many approaches to combining genes. Our code creates offspring using uniform crossover in which each gene has an equal chance of being chosen from one of the parents. Other strategies may favor one parent’s genes over another. Another popular strategy is k-point crossover, in which chromosomes are split at k points resulting in
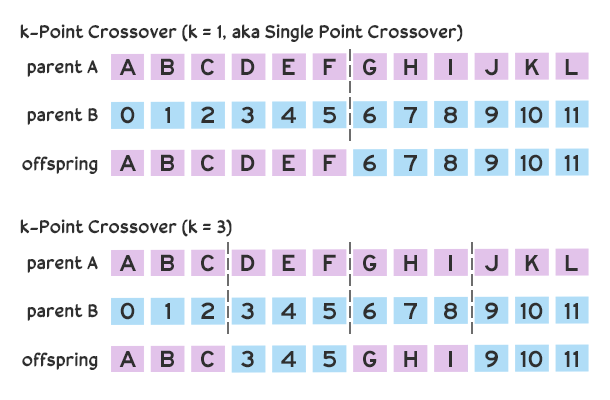
We’re also not limited to two parent chromosomes; we combine genes from three or more candidates, or even build off a single candidate. Consider an algorithm written to evolve an image by drawing random polygons. In this case, our chromosomes are implemented as image data. During each generation, the fittest image is selected from the population and serves as the parent, and all children candidates are generated by drawing their own polygons to a copy of parent. The parent chromosome/image serves as a base and children chromosomes/images are unique mutations/drawings on the parent.
Genetic Algorithms in Action
Genetic algorithms can be use for both fun and profit. Perhaps two of the most popular examples of genetic algorithms in action are BoxCar 2D and NASA’s evolved X-band antennas.
BoxCar 2D is a simulation that uses genetic algorithms to evolve the best “car” capable of traversing simulated terrain. The car is constructed from eight random vectors creating a polygon and attaching and wheels to random points. The project’s website can be found at boxcar2d.com, which offers a brief write-up of the algorithm in its about page and a leaderboard showcasing some of the best designs. Unfortunately, the site uses Flash, which may make it inaccessible for many now — in which case you can find various screen recordings on YouTube if you’re curious. You may also want to check out a similar (excellent) simulation written by Rafael Matsunaga using HTML5 technologies available at rednuht.org/genetic_cars_2.
In 2006, NASA’s Space Technology 5 mission tested various new technologies in space. One such technology was new antennas designed using genetic algorithms. Designing a new antenna can be a very expensive and time-consuming process. It requires special expertise, and frequent setbacks happen when requirements change or prototypes don’t perform as expected. The evolved antennas took less time to create, had higher gain, and used less power. The full text of the paper discussing the design process is freely available online (Automated Antenna Design with Evolutionary Algorithms). Genetic algorithms have also been used to optimize existing antenna designs for greater performance.

Genetic algorithms have even been used in web design! A senior project by Elijah Mensch (Optimizing Website Design Through the Application of an Interactive Genetic Algorithm) used them to optimize a news article carousel by manipulating CSS rules and scoring fitness with A/B testing.
Conclusion
By now, you should posses a basic understanding of what genetic algorithms are and be familiar enough with their vocabulary to decipher any resources you may come across in your own research. But understanding theory and terminology is only half the work. If you plan to write your own genetic algorithm, you have to understand your particular problem as well. Here are some important questions to ask yourself before you get started:
-
How can I represent my problem as chromosomes? What are my valid alleles?
-
Do I know what the target is? That is, what am I looking for? Is it a specific value or any solution that has a fitness beyond a certain threshold?
-
How can I quantify the fitness of my candidates?
-
How can I combine and mutate candidates to produce new candidate solutions?
I hope I’ve also helped you to find an appreciation for how programs can draw inspiration from nature — not just in form, but also in process and function. Feel free to share your own thoughts in the forums.
FAQs About Genetic Algorithms
A Genetic Algorithm is a heuristic search and optimization technique inspired by the process of natural selection. It is used to find approximate solutions to optimization and search problems by mimicking the principles of evolution.
Genetic Algorithms work by evolving a population of candidate solutions over successive generations. The process involves selection, crossover (recombination), mutation, and evaluation of individuals in the population, aiming to iteratively improve the quality of solutions.
Genetic Algorithms are versatile and can be applied to various optimization and search problems, including but not limited to scheduling, routing, machine learning, and function optimization.
Parameters like population size, mutation rate, and crossover rate depend on the specific problem and characteristics of the solution space. Experimentation and tuning are common practices to find optimal parameter values for a given problem.
The fitness function quantifies how well an individual solution performs in the given problem. It guides the selection process, favoring solutions that contribute positively to the optimization goal.
Timothy Boronczyk is a native of Syracuse, New York, where he lives with no wife and no cats. He has a degree in Software Application Programming, is a Zend Certified Engineer, and a Certified Scrum Master. By day, Timothy works as a developer at ShoreGroup, Inc. By night, he freelances as a writer and editor. Timothy enjoys spending what little spare time he has left visiting friends, dabbling with Esperanto, and sleeping with his feet off the end of his bed.

