Fundamental Concepts

Introduction

What is a distributed system and why we need it

First of all, we need to define what a distributed system is. Multiple, different definitions can be found, but we will use the following:

"A distributed system is a system whose components are located on different networked computers, which communicate and coordinate their actions by passing messages to one another."[1]

As shown in Figure 1, this network can either consist of direct connections between the components of the distributed system or there could be more components that form the backbone of the network (if communication is done through the Internet for example). These components can take many forms; they could be servers, routers, web browsers or even mobile devices. In an effort to keep an abstract and generic view, in the context of this book we'll refer to them as nodes, being agnostic to their real form. In some cases, such as when providing a concrete example, it might be useful to escape this generic view and see how things work in real-life. In these cases, we might explain in detail the role of each node in the system.

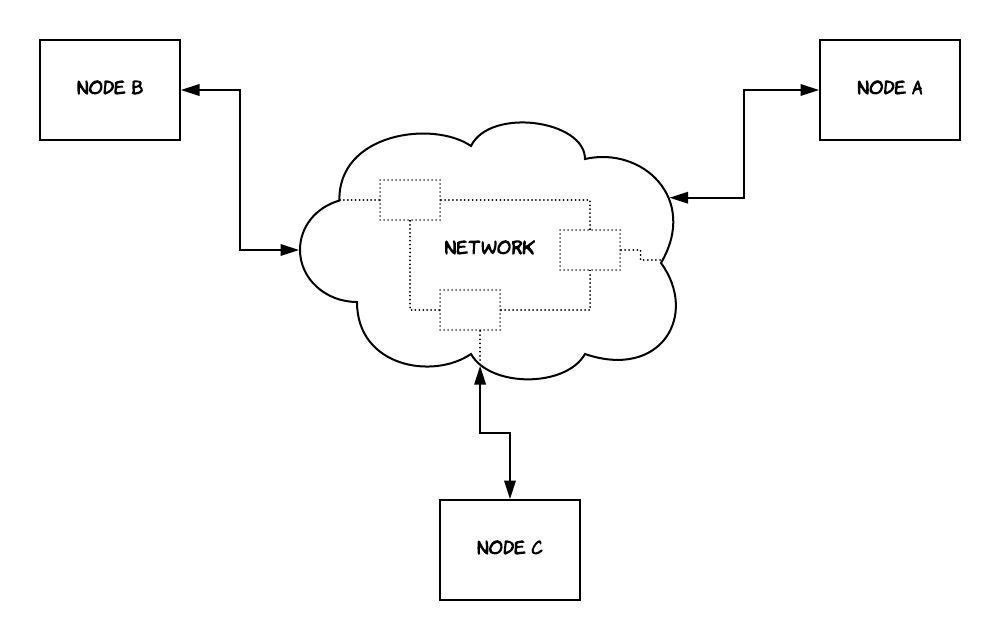
Figure 1: A distributed system

As we will see later, the 2 parts that were highlighted in the definition above are central to how distributed systems function:

• the various parts that compose a distributed system are located remotely, separated by a network.
• the main mechanism of communication between them is by exchanging messages, using this network that separates them.

Now that we have defined what a distributed system is, let's explore its value.

Why do we really need distributed systems ?

Looking at all the complexity that distributed systems introduce, as we will see during this book, that's a valid question. The main benefits of distributed systems come mostly in the following 3 areas:

• performance
• scalability
• availability

Let's explain each one separately. The performance of a single computer has certain limits imposed by physical constraints on the hardware. Not only that, but after a point, improving the hardware of a single computer in order to achieve better performance becomes extremely expensive. As a result, one can achieve the same performance with 2 or more low-spec computers as with a single, high-end computer. So, distributed systems allow us to achieve better performance at a lower cost. Note that better performance can translate to different things depending on the context, such as lower latency per request, higher throughput etc.

"Scalability is the capability of a system, network, or process to handle a growing amount of work, or its potential to be enlarged to accommodate that growth." [2]

Most of the value derived from software systems in the real world comes from storing and processing data. As the customer base of a system grows, the system needs to handle larger amounts of traffic and store larger amounts of data. However, a system composed of a single computer can only scale up to a certain point, as explained previously. Building a distributed system allows us to split and store the data in multiple computers, while also distributing the processing work amongst them¹. As a result of this, we are capable of scaling our systems to sizes that would not even be imaginable with a single-computer system.

In the context of software systems, availability is the probability that a system will work as required when required during the period of a mission. Note that nowadays most of the online services are required to operate all the time (known also as 24/7 service), which makes this a huge challenge. So, when a service states that it has 5 nines of availability, this means that it operates normally for 99.999% of the time. This implies that it's allowed to be down for up to 5 minutes a year, to satisfy this guarantee. Thinking about how unreliable hardware can be, one can easily understand how big an undertaking this is. Of course, using a single computer, it would be infeasible to provide this kind of guarantees. One of the mechanisms that are widely used to achieve higher availability is redundancy, which means storing data into multiple, redundant computers. So, when one of them fails, we can easily and quickly switch to another one, preventing our customers from experiencing this failure. Given that data are stored now in multiple computers, we end up with a distributed system!

Leveraging a distributed system we can get all of the above benefits. However, as we will see later on, there is a tension between them and several other properties. So, in most of the cases we have to make a trade-off. To do this, we need to understand the basic constraints and limitations of distributed systems, which is the goal of the first part of this book.

The fallacies of distributed computing

Distributed systems are subject to many more constraints, when compared to software systems that run in a single computer. As a result, developing software for distributed systems is also very different. However, people that are new to distributed systems make assumptions, based on their experience developing software for systems that run on a single computer. Of course, this creates a lot of problems down the road for the systems they build. In an effort to eliminate this confusion and help people build better systems, L Peter Deutsch and others at Sun Microsystems created a collection of these false assumptions, which is now known as the fallacies of distributed computing². These are the following:

1. The network is reliable.[3][4]
2. Latency is zero.
3. Bandwidth is infinite.
4. The network is secure.
5. Topology doesn't change.
6. There is one administrator.
7. Transport cost is zero.
8. The network is homogeneous.

As you progress through the book, you will get a deeper understanding of why these statements are fallacies. However, we will try and give you a sneak preview here by going quickly over them and explain where they fall short. The first fallacy is sometimes enforced by abstractions provided to developers from various technologies and protocols. As we will see in a later chapter networking protocols, such as TCP, can make us believe that the network is reliable and never fails, but this is just an illusion and can have significant repercussions. Network connections are also built on top of hardware that will also fail at some point and we should design our systems accordingly. The second assumption is also enforced nowadays by libraries, which attempt to model remote procedure calls as local calls, such as gRPC ³ or Thrift ⁴. We should always keep in mind that there is a difference of several orders of magnitude in latency between a call to a remote system and a local memory access (from milliseconds to nanoseconds). This is getting even worse, when we are talking about calls between datacenters in different continents, so this is another thing to keep in mind when deciding about how we want to geo-distribute our system. The third one is getting weaker nowadays, since there have been significant improvements in the bandwidth that can be achieved during the last decades. Still, even though we can build high-bandwidth connections in our own datacenter, this does not mean that we will be able to use all of it, if our traffic needs to cross the Internet. This is an important consideration to keep in mind, when making decisions about the topology of our distributed system and when requests will have to travel through the Internet. The fourth fallacy illustrates the fact that the wider network that is used by two nodes in order to communicate is not necessarily under their control and thus should be considered insecure. The book contains a chapter dedicated on security that explains various techniques that can be used in order to make use of this insecure network in a secure way. This network is also composed of many different parts that might be managed by different organisations with potentially different hardware and failures in some parts of this network might mean its topology might have to change to remain functional. This is all highlighted by the fifth, sixth and eighth fallacies. Last but not least, transportation of data between two points incurs financial costs, which should be factored in when building a distributed system.

There's one more fallacy that's not included in the above set, but it's still very common amongst people new to distributed systems and can also create a lot of confusion. If we were to follow the same style as above, we would probably phrase it in the following way:

"Distributed systems have a global clock, which can be used to identify when events happen."

This assumption can be quite deceiving, since it's somewhat intuitive and holds true when working in systems that are not distributed. For instance, an application that runs in a single computer can use the computer's local clock in order to decide when events happen and what's the order between them. Nonetheless, that's not true in a distributed system, where every node in the system has its own local clock, which runs at a different rate from the other ones. There are ways to try and keep the clocks in sync, but some of them are very expensive and do not eliminate these differences completely. This limitation is again bound by physical laws ⁵. An example of such an approach is the TrueTime API that was built by Google [5], which exposes explicitly the clock uncertainty as a first-class citizen. However, as we will see in the next chapters of the book, when one is mainly interested in cause and effects, there are other ways to reason about time using logical clocks instead.

Why distributed systems are hard

In general, distributed systems are hard to design, build and reason about, thus increasing the risk of error. This will become more evident later in the book while exploring some algorithms that solve fundamental problems that emerge in distributed systems. It's worth questioning: why are distributed systems so hard? The answer to this question can help us understand what are the main properties that make distributed systems challenging, thus eliminating our blind spots and providing some guidance on what are some of the aspects we should be paying attention to.

The main properties of distributed systems that make them challenging to reason about are the following:

• network asynchrony
• partial failures
• concurrency

Network asynchrony is a property of communication networks that cannot provide strong guarantees around delivery of events, e.g. a maximum amount of time required for a message to be delivered. This can create a lot of counter-intuitive behaviours that would not be present in non-distributed systems. This is in contrast to memory operations that can provide much stricter guarantees ⁶. For instance, in a distributed system messages might take extremely long to be delivered, they might be delivered out of order or not at all.

Partial failures are cases where only some components of a distributed system fail. This behaviour can come in contrast to certain kinds of applications deployed in a single server that work under the assumption that either the whole server has crashed or everything is working fine. It introduces significant complexity when there is a requirement for atomicity across components in a distributed system, i.e. we need to ensure that an operation is either applied to all the nodes of a system or to none of them. The chapter about distributed transactions analyses this problem.

Concurrency is execution of multiple computations happening at the same time and potentially on the same piece of data interleaved with each other. This introduces additional complexity, since these different computations can interfere with each other and create unexpected behaviours. This is again in contrast to simplistic applications with no concurrency, where the program is expected to run in the order defined by the sequence of commands in the source code. The various types of problematic behaviours that can arise from concurrency are explained in the chapter that talks about isolation later in the book.

As explained, these 3 properties are the major contributors of complexity in the field of distributed systems. As a result, it will be useful to keep them in mind during the rest of the book and when building distributed systems in real life so that you can anticipate edge cases and handle them appropriately.

Correctness in distributed systems

The correctness of a system can be defined in terms of the properties it must satisfy. These properties can be of the following types:

• Safety properties
• Liveness properties

A safety property defines something that must never happen in a correct system, while a liveness property defines something that must eventually happen in a correct system. As an example, considering the correctness properties of an oven, we could say that the property of "the oven not exceeding a maximum temperature threshold" is a safety property. The property of "the oven eventually reaching the temperature we specified via the button" is a liveness property. Similar to this example, in distributed systems, it's usually more important to make sure that the system satisfies the safety properties than the liveness ones. Throughout this book, it will become clear that there is an inherent tension between safety and liveness properties. Actually, as we will see later in the book, there are some problems, where it's physically impossible to satisfy both kinds of properties, so compromises are made for some liveness properties in order to maintain safety.

System models

Real-life distributed systems can differ drastically in many dimensions, depending on the network where they are deployed, the hardware they are running on etc. Thus, we need a common framework so that we can solve problems in a generic way without having to repeat the reasoning for all the different variations of these systems. In order to do this, we can create a model of a distributed system by defining several properties that it must satisfy. Then, if we prove an algorithm is correct for this model, we can be sure that it will also be correct for all the systems that satisfy these properties.

The main properties that are of interest in a distributed system have to do with:

• how the various nodes of a distributed system interact with each other
• how a node of a distributed system can fail

Depending on the nature of communication, we have 2 main categories of systems: synchronous and asynchronous systems. A synchronous system is one, where each node has an accurate clock and there is a known upper bound on message transmission delay and processing time. As a result, the execution is split into rounds so that every node can send a message to another node, the messages are delivered and every node computes based on the messages just received, all nodes running in lock-step. An asynchronous system is one, where there is no fixed upper bound on how long it takes for a message to be delivered or how much time elapses between consecutive steps of a node. The nodes of the system do not have a common notion of time and thus run in independent rates. The challenges arising from network asynchrony have already been discussed previously. So, it should be clear by now that the first model is much easier to describe, program and reason about. However, the second model is closer to real-life distributed systems, such as the Internet, where we cannot have control over all the components involved and there are very limited guarantees on the time it will take for a message to be sent between two places. As a result, most of the algorithms we will be looking at this book assume an asynchronous system model.

There are also several different types of failure. The most basic categories are:

• Fail-stop: A node halts and remains halted permanently. Other nodes can detect that the node has failed (i.e. by communicating with it).
• Crash: A node halts and remains halted, but it halts in a silent way. So, other nodes may not be able to detect this state (i.e. they can only assume it has failed on the basis of not being able to communicate with it).
• Omission: A node fails to respond to incoming requests.
• Byzantine: A node exhibits arbitrary behavior: it may transmit arbitrary messages at arbitrary times, it may stop or take an incorrect step.

Byzantine failures can be exhibited, when a node does not behave according to the specified protocol/algorithm, i.e. because the node has been compromised by a malicious actor or because of a software bug. Coping with these failures introduces significant complexity to the resulting solutions. At the same time, most distributed systems in companies are deployed in environments that are assumed to be private and secure. Fail-stop failures are the simplest and the most convenient ones from the perspective of someone that builds distributed systems. However, they are also not very realistic, since there are cases in real-life systems where it's not easy to identify whether another node has crashed or not. As a result, most of the algorithms analysed in this book work under the assumption of crash failures.

The tale of exactly-once semantics

As described in the beginning of the book, the various nodes of a distributed system communicate with each other by exchanging messages. Given that the network is not reliable, these messages might get lost. Of course, to cope with this, nodes can retry sending them hoping that the network will recover at some point and deliver the message. However, this means that messages might be delivered multiple times, as shown in Figure 2, since the sender can't know what really happened.

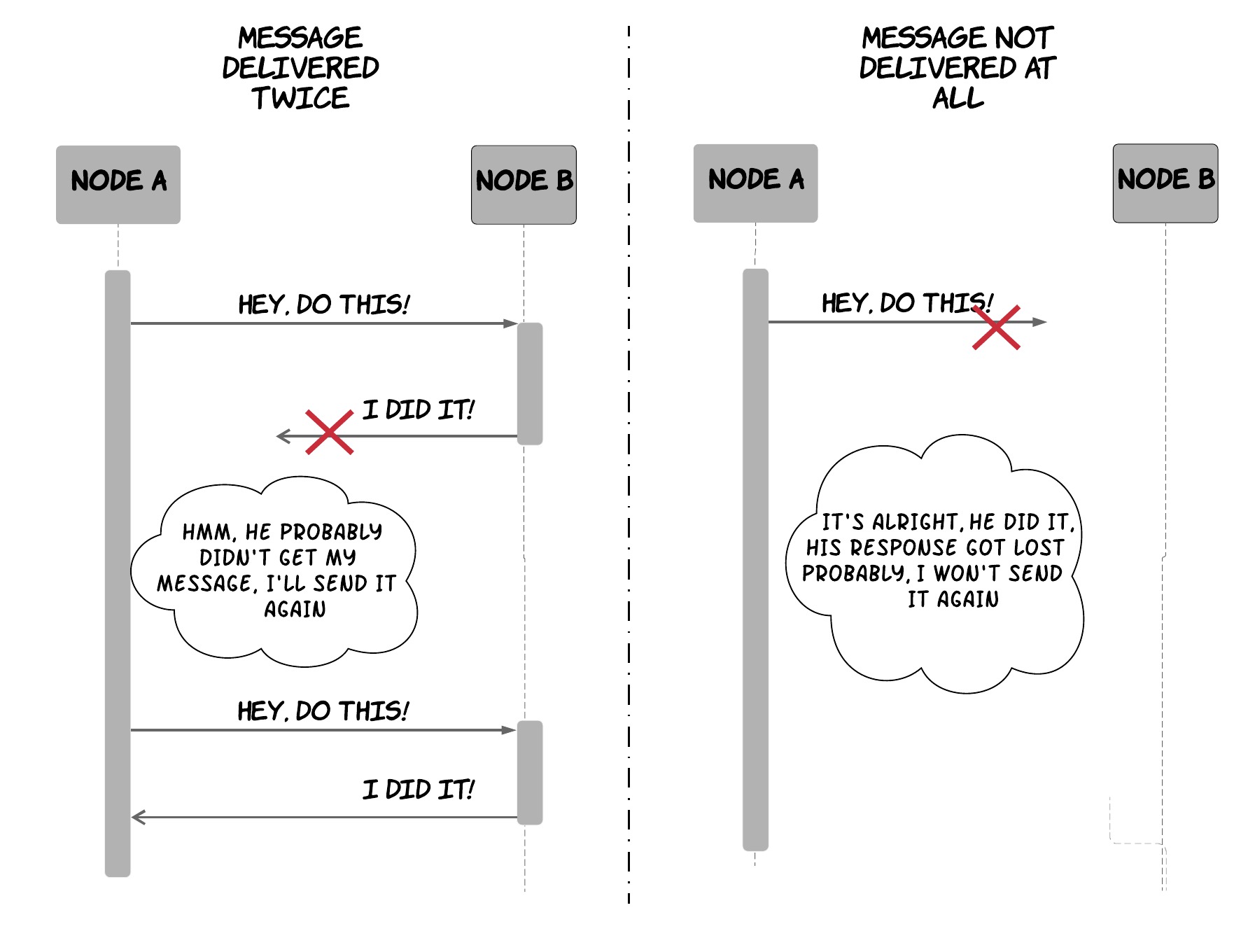
Figure 2: Intricacies of a non-reliable network in distributed systems

This duplicate delivery of a message can create disastrous side-effects. For instance, think what would happen if that message is supposed to signal transfer of money between 2 bank accounts as part of a purchase; a customer might be charged twice for a product. To handle scenarios like this, there are multiple approaches to ensure that the processing of a message will only be done once, even though it might be delivered multiple times.

One approach is using idempotent operations. Idempotent is an operation that can be applied multiple times without changing the result beyond the initial application. An example of an idempotent operation is adding a value in a set of values. Even if this operation is applied multiple times, the applications that follow the first one will have no effect, since the value will already have been added in the set. Of course, this is under the assumption that other operations cannot remove values from the set. Otherwise, the retried operation might add a value that had been removed in the meanwhile. On the contrary, an example of a non-idempotent operation would be increasing a counter by one, which has additional side-effects every time it's applied. By making use of idempotent operations, we can have a guarantee that even if a message is delivered multiple times and the operation is repeated, the end result will be the same.

However, as demonstrated previously idempotent operations commonly impose tight constraints on the system. So, in many cases we cannot build our system, so that all operations are idempotent by nature. In these cases, we can use a de-duplication approach, where we give every message a unique identifier and every retried message contains the same identifier as the original. In this way, the recipient can remember the set of identifiers it has received and executed already and avoid executing operations that have already been executed. It is important to note that in order to do this, one must have control on both sides of the system (sender and receiver). This is due to the fact that the ID generation is done on the sender side, but the deduplication process is done on the receiver side. As an example, imagine a scenario where an application is sending emails as part of an operation. Sending an e-mail is not an idempotent operation, so if the e-mail protocol does not support de-duplication on the receiver side, then we cannot be absolutely sure that every e-mail is shown exactly once to the recipient.

When thinking about exactly-once semantics, it's useful to distinguish between the notions of delivery and processing. In the context of this discussion, let's consider delivery being the arrival of the message at the destination node at the hardware level. Then, we consider processing being the handling of this message from the software application layer of the node. In most cases, what we really care about is how many times a message is processed, not how many times it has been delivered. For instance, in our previous e-mail example, we are mainly interested in whether the application will display the same e-mail twice, not whether it will receive it twice. As the previous examples demonstrated, it's impossible to have exactly-once delivery in a distributed system. It's still sometimespossible though to have exactly-once processing. With all that said, it's important to understand the difference between these 2 notions and make clear what you are referring to, when you are talking about exactly-once semantics.

Also, as a last note, it's easy to see that at-most-once delivery semantics and at-least-once delivery semantics can be trivially implemented. The former can be achieved by sending every message only one time no matter what happens, while the latter one can be achieved by sending a message continuously, until we get an acknowledgement from the recipient.

Failure in the world of distributed systems

It is also useful to understand that it is very difficult to identify failure because of all the characteristics of a distributed system described so far. The asynchronous nature of the network in a distributed system can make it very hard to differentiate between a node that has crashed and a node that is just really slow to respond to requests. The main mechanism used to detect failures in a distributed systems are timeouts. Since messages can get infinitely delayed in an asynchronous network, timeouts impose an artificial upper bound on these delays. As a result, when a node is slower than this bound, we can assume that the node has failed. This is useful, since otherwise the system might be blocked eternally waiting for nodes that have crashed under the assumption that they might just be extremely slow.

However, this timeout does not represent an actual limit, so it creates the following trade-off. Selecting a smaller value for this timeout means that our system will waste less time waiting for nodes that have crashed. At the same time, the system might be declaring dead some nodes that have not crashed, but they are just being a bit slower than expected. On the other hand, selecting a larger value for this timeout means that the system will be more lenient with slow nodes. However, it also implies that the system will be slower in identifying crashed nodes, thus wasting time waiting for them in some cases. This is illustrated in Figure 3.

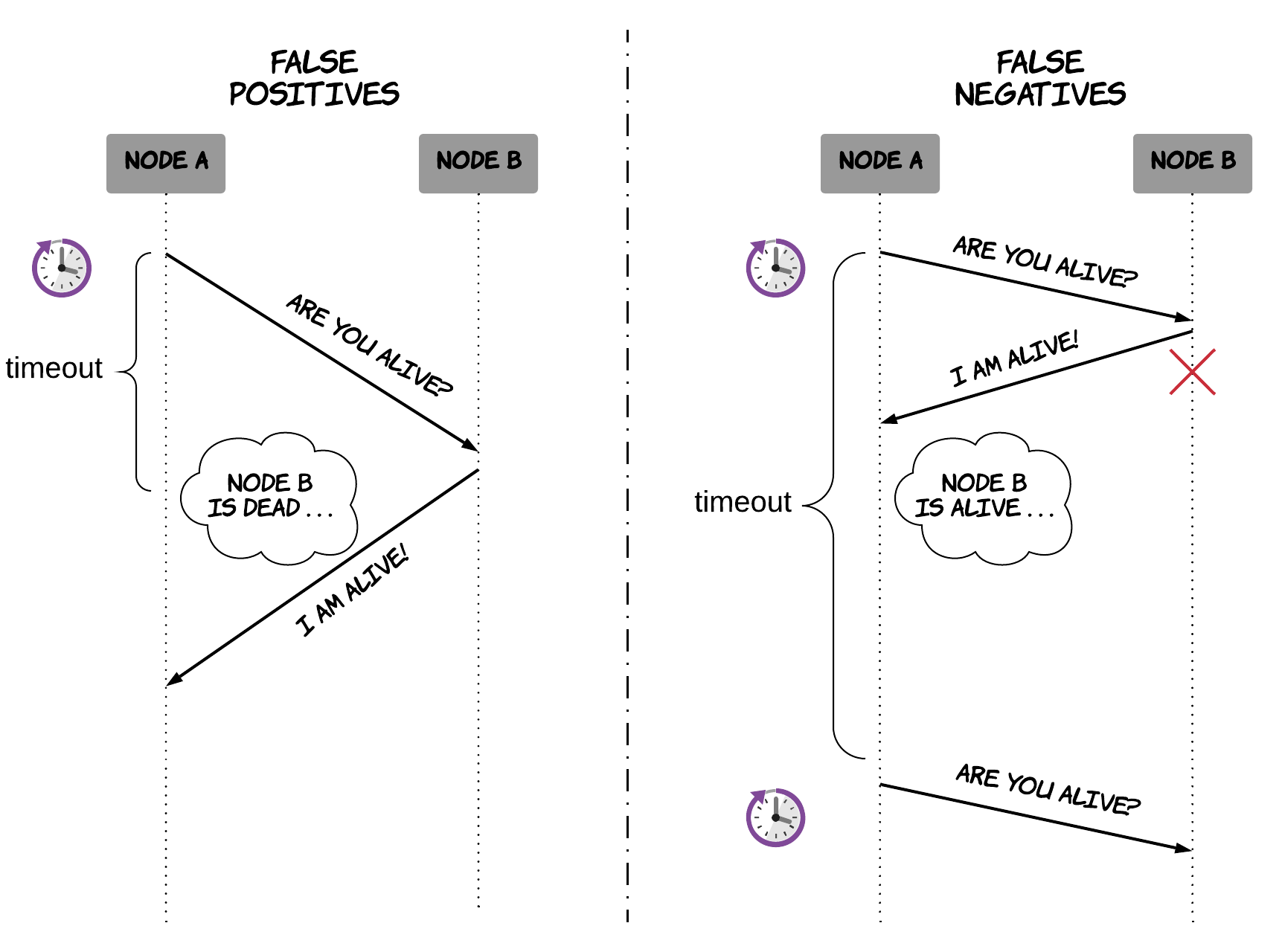
Figure 3: Trade-offs in failure detection

In fact, this is a very important problem in the field of distributed systems. The component of a node that is used to identify other nodes that have failed is called a failure detector. As we explained previously, this component is very important for various algorithms that need to make progress in the presence of failures. There has been extensive research about failure detectors [6]. The different categories of failure detectors are distinguished by 2 basic properties that reflect the aforementioned trade-off: completeness and accuracy. Completeness corresponds to the percentage of crashed nodes a failure detector succeeded in identifying in a certain period. Accuracy corresponds to the number of mistakes a failure detector made in a certain period. A perfect failure detector is one that is characterised by the strongest form of completeness and accuracy, namely one that can successfully detect every faulty process without ever thinking a node has crashed before it actually crashes. As expected, it is impossible to build a perfect failure detector in purely asynchronous systems. Still, even imperfect failure detectors can be used to solve difficult problems, such as the problem of consensus which is described later.

Stateful and Stateless systems

We could say that a system can belong in one of the 2 following categories:

• stateless systems
• stateful systems

A stateless system is one that maintains no state of what has happened in the past and is capable of performing its capabilities, purely based on the inputs provided to it. For instance, a contrived stateless system is one that receives a set of numbers as input, calculates the maximum of them and returns it as the result. Note that these inputs can be direct or indirect. Direct inputs are those included in the request, while indirect inputs are those potentially received from other systems to fullfil the request. For instance, imagine a service that calculates the price for a specific product by retrieving the initial price for it and any currently available discounts from some other services and then performing the necessary calculations with this data. This service would still be stateless. On the other hand, stateful systems are responsible for maintaining and mutating some state and their results depend on this state. As an example, imagine a system that stores the age of all the employees of a company and can be asked for the employee with the maximum age. This system is stateful, since the result depends on the employees we've registered so far in the system.

There are some interesting observations to be made about these 2 types of systems:

• Stateful systems can be really useful in real-life, since computers are much more capable in storing and processing data than humans.
• Maintaining state comes with additional complexity, such as deciding what's the most efficient way to store it and process it, how to perform back-ups etc.
• As a result, it's usually wise to create an architecture that contains clear boundaries between stateless components (which are performing business capabilities) and stateful components (which are responsible for handling data).
• Last and most relevant to this book, it's much easier to design, build and scale distributed systems that are stateless when compared to stateful ones. The main reason for this is that all the nodes (e.g. servers) of a stateless system are considered to be identical. This makes it a lot easier to balance traffic between them and scale by adding or removing servers. However, stateful systems present many more challenges, since different nodes can hold different pieces of data, thus requiring additional work to direct traffic to the right place and ensure each instance is in sync with the other ones.

As a result, some of the book's examples might include stateless systems, but the most challenging problems we will cover in this book are present mostly in stateful systems.

Basic concepts and theorems

Partitioning

As we described previously, one of the major benefits of distributed systems is scalability, allowing us to store and process datasets much larger than what one could do with a single machine. One of the primary mechanisms of achieving scalability, is called partitioning. Partitioning is the process of splitting a dataset into multiple, smaller datasets and then assigning the responsibility of storing and processing them to different nodes of a distributed system. This allows us to increase the size of the data our system can handle, by adding more nodes to the system.

There are 2 different variations of partitioning: vertical partitioning and horizontal partitioning (also called sharding). The terms vertical and horizontal originate from the era of relational databases, which established the notion of a tabular view of data. ⁷ In this view, data consist of rows and columns, where a row is a different entry in the dataset and each column is a different attribute for every entry. Figure 4 contains a visual depiction of the difference between these 2 approaches.

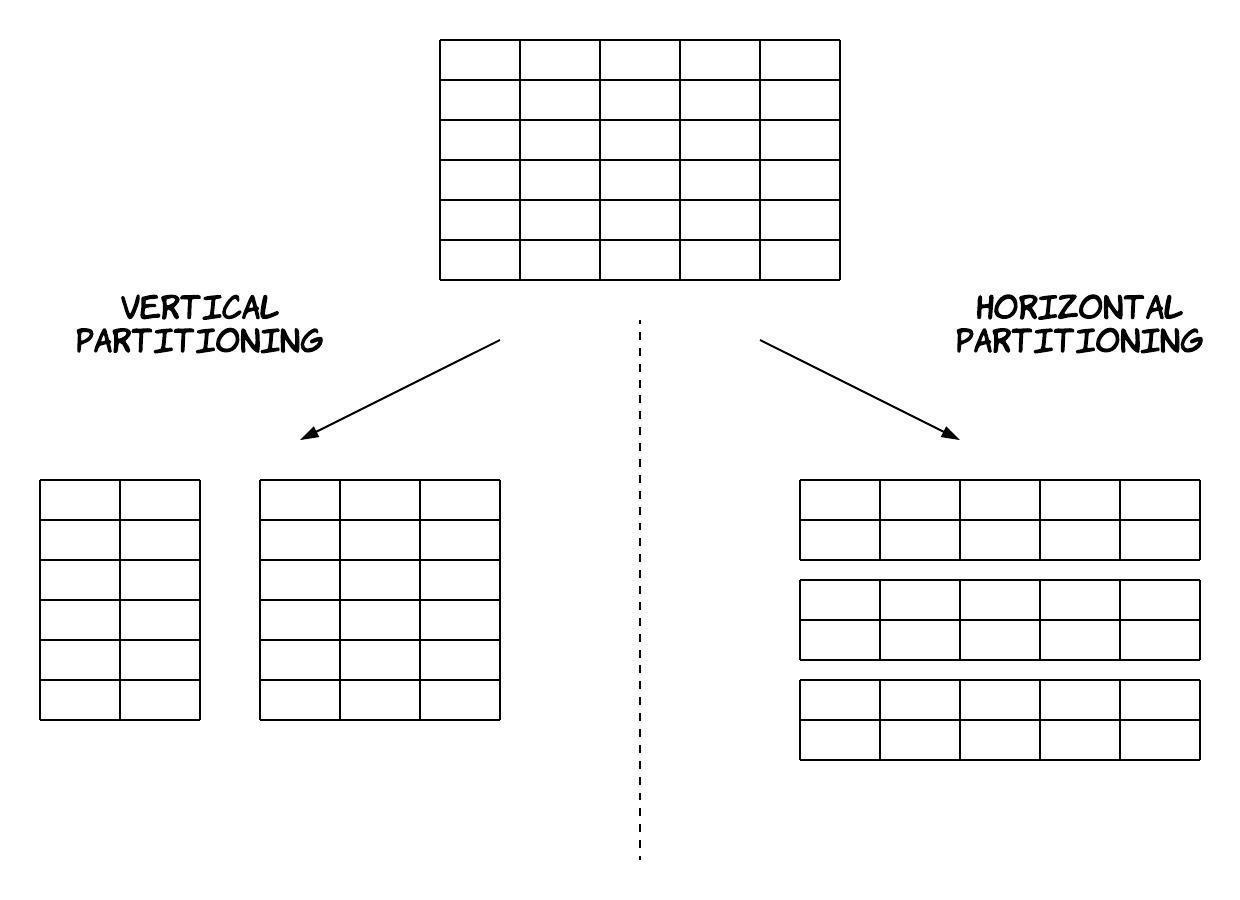
Figure 4: Vertical and Horizontal Partitioning

Vertical partitioning involves splitting a table into multiple tables with fewer columns and using additional tables to store columns that serve the purpose of relating rows across tables (commonly referred to as a join operation). These different tables can then be stored in different nodes. Normalization ⁸ is one way to perform vertical partitioning, but general vertical partitioning can go far beyond that, splitting columns, even when they are normalized.

On the other hand, horizontal partitioning involves splitting a table into multiple, smaller tables, where each of those tables contain a percentage of the rows of the initial table. These different sub-tables can then be stored in different nodes. There are multiple strategies for performing this split, as we will see later on. A simplistic approach is an alphabetical split. For instance, in a table containing the students of a school, we could partition horizontally, using the surname of the students, as shown in Figure 5.

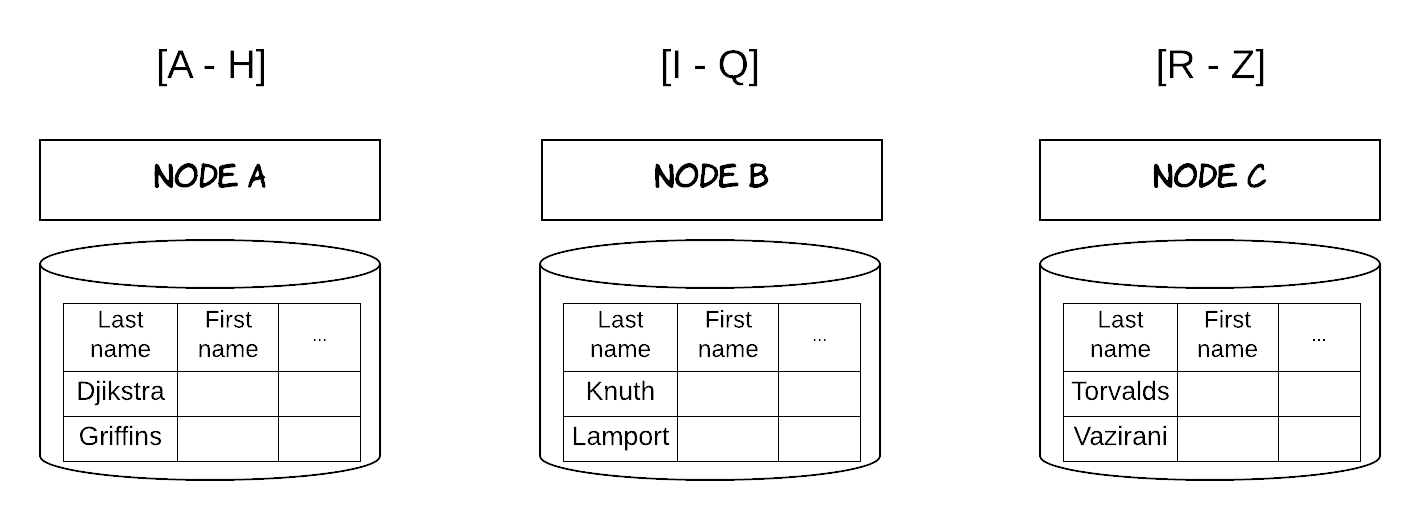
Figure 5: Horizontal Partitioning using alphabetical order

Partitioning helps with allowing a system to handle larger datasets more efficiently, but it also introduces some limitations. In a vertically partitioned system, requests that need to combine data from different tables (i.e. join operations) become less efficient, because these requests might now have to access data from multiple nodes. In a horizontally partitioned system, this is usually avoided, because all the data for each row is located in the same node. However, it can happen for requests that are searching for a range of rows and these rows belong to multiple nodes. Another important implication of horizontal partitioning is the potential for loss of transactional semantics. When storing data in a single machine, it's easy to perform multiple operations in an atomic way, so that either all of them succeed or none of them succeeds, but this is much harder to achieve in a distributed system (as we will see in the chapter about distributed transactions). As a result, when partitioning data horizontally, it's much harder to perform atomic operations over data that reside in different nodes. This is a common theme in distributed systems; there's no silver bullet, one has to make trade-offs in order to achieve a desired property.

Vertical partitioning is mainly a data modelling practice, which can be performed by the engineers designing a system, sometimes independently of the storage systems that will be used. However, horizontal partitioning is commonly provided as a feature of distributed databases, so it's important for engineers to know how it works under the hood in order to make proper use of these systems. As a result, we will focus mostly on horizontal partitioning in this book.

Algorithms for horizontal partitioning

There are a lot of different algorithms for performing horizontal partitioning. In this section, we will study some of these algorithms, discussing the advantages and drawbacks of each one.

Range partitioning is a technique, where a dataset is split into ranges, according to the value of a specific attribute. Each range is then stored in a separate node. The case we described previously with the alphabetical split is an example of range partitioning. Of course, the system should store and maintain a list of all these ranges, along with a mapping, indicating which node stores a specific range. In this way, when the system is receiving a request for a specific value (or a range of values), it consults this mapping to identify to which node (or nodes, respectively) the request should be redirected.

The advantages of this technique are:

• its simplicity and ease of implementation.
• the ability to perform range queries, using the value that is used as the partitioning key.
• a good performance for range queries using the partitioning key, when the queried range is small and resides in a single node.
• easy and efficient way to adjust the ranges (re-partition), since one range can be increased or decreased, exchanging data only between 2 nodes.

Some of its disadvantages are:

• the inability to perform range queries, using other keys than the partitioning key.
• a bad performance for range queries using the partitioning key, when the queried range is big and resides in multiple nodes.
• an uneven distribution of the traffic or the data, causing some nodes to be overloaded. For example, some letters are more frequent as initial letters in surnames, ⁹ which means that some nodes might have to store more data and process more requests.

Some systems that leverage a range partitioning technique are Google's BigTable [7] and Apache HBase. ¹⁰

Hash partitioning is a technique, where a hash function is applied to a specific attribute of each row, resulting in a number that determines which partition (and thus node) this row belongs to. For the sake of simplicity, let's assume we have one partition per node (as in the previous example) and a hash function that returns an integer. If we have n number of nodes in our system and trying to identify which node a student record with a surname s is located at, then we could calculate it using the formula hash(s) mod n. This mapping process needs to be done both when writing a new record and when receiving a request to find a record for a specific value of this attribute.

The advantages of this technique are:

• the ability to calculate the partitioning mapping at runtime, without needing to store and maintain the mapping. This has benefits both in terms of data storage needs and performance (since no additional request is needed to find the mapping).
• a bigger chance of the hash function distributing the data more uniformly across the nodes of our system, thus preventing some nodes from being overloaded.

Some disadvantages of this technique are:

• the inability to perform range queries at all (even for the attribute used as a partitioning key), without storing additional data or querying all the nodes.
• adding/removing nodes from the systems causes re-partitioning, which results in significant movement of data across all nodes of the system.

Consistent hashing is a partitioning technique, having very similar characteristics to the previous one, but solving the problem of increased data movement during re-partitioning. The way it works is the following: each node in the system is randomly assigned an integer in a range [0, L], called ring (i.e. [0, 360]). Then, a record with a value s for the attribute used as partitioning key is located to the node that is the next one after the point hash(s) mod L in the ring. As a result, when a new node is added to the ring, it receives data only from the previous node in the ring, without any more data needed to be exchanged between any other nodes. In the same way, when a node is removed from the ring, its data just need to be transferred to the next node in the ring. For a visual representation of this behaviour and the difference between these 2 different algorithms, see Figure 6.

Some disadvantages of this technique are:

• the potential for non-uniform distribution of the data, because of the random assignment of the nodes in the ring.
• the potential for creating more imbalanced data distribution as nodes are added or removed. For example, when a node is removed, its dataset is not distributed evenly across the system, but it's transferred to a single node.

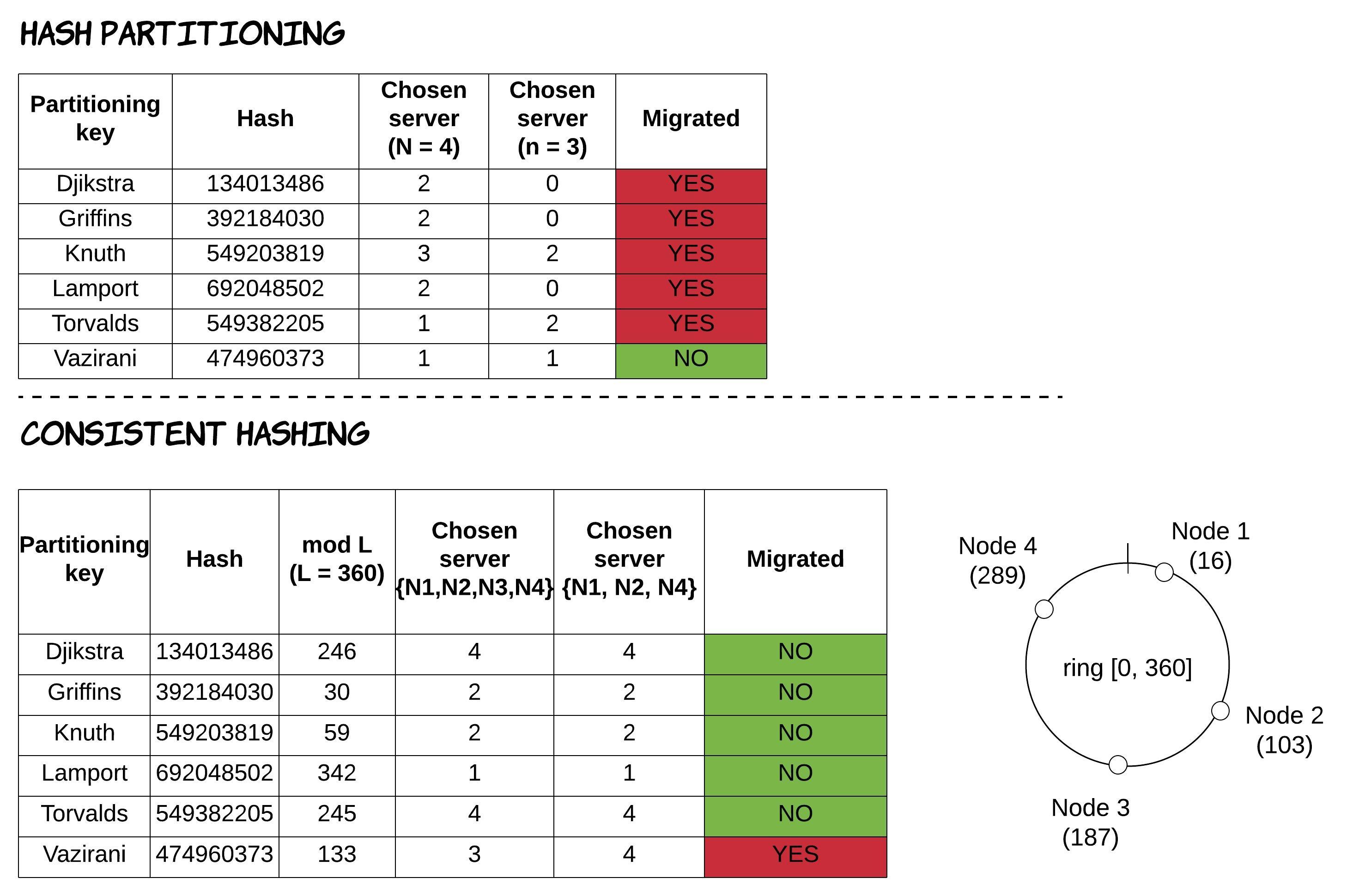
Figure 6: Re-partitioning, when a node (N3) is removed, in hash partitioning and consistent hashing

Both of these issues can be mitigated by using the concept of "virtual nodes", where each physical node is assigned multiple locations (virtual nodes) in the ring. For more discussion on this concept, feel free to read the Dynamo paper [8]. Another widely used system that makes use of consistent hashing is Apache Cassandra [9].

Replication

As we discussed in the previous section, partitioning can improve the scalability and performance of a system, by distributing data and request load to multiple nodes. However, the introduction mentioned another dimension that benefits from the usage of a distributed system and that was availability. This property directly translates to the ability of the system to remain functional despite failures in parts of it. Replication is the main technique used in distributed systems in order to increase availability. It consists of storing the same piece of data in multiple nodes (called replicas), so that if one of them crashes, data is not lost and requests can be served from the other nodes in the meanwhile.

However, the benefit of increased availability from replication comes with a set of additional complications. Replication implies that the system now has multiple copies of every piece of data, which must be maintained and kept in sync with each other on every update. Ideally, replication should function transparently to the end-user (or engineer), creating the illusion that there is only a single copy of every piece of data. This makes a distributed system look like a simple, centralised system of a single node, which is much easier to reason about and develop software around.

Of course, this is not always possible; it might require significant hardware resources or giving up other desired properties to achieve this ideal. For instance, engineers are sometimes willing to accept a system that provides much higher performance, giving occasionally a non-consistent view of the data as long as this is done only under specific conditions and in a specific way they can account for, when designing the overall application. As a result of this, there are 2 main strategies for replication:

• Pessimistic replication: this strategy tries to guarantee from the beginning that all of the replicas are identical to each other, as if there was only a single copy of the data all along.
• Optimistic replication (also called lazy replication): this strategy allows the different replicas to diverge, guaranteeing that they will converge again if the system does not receive any updates (also known as quiesced) for a period of time.

Replication is a very active field in research, so there are many different algorithms. As an introduction, we will now discuss the 2 main techniques: single-master replication and multi-master replication.

Single-master replication

Single-master replication is a technique, where a single node amongst the replicas is designated as master (or primary) and is responsible for receiving all the updates ¹¹. The remaining replicas are commonly referred to as slaves (or secondaries) and they can only handle read requests. Every time the master receives an update, it's responsible for propagating this update to the other nodes besides executing it locally, ensuring all the replicas will maintain a consistent view of the data. This propagation of the updates can be done in 2 ways: either synchronously or asynchronously.

In synchronous replication, the node can reply to the client indicating the update has been completed, only after having received acknowledgements from the other replicas that they have also performed the update on their local storage. This guarantees that after an update has been acknowledged to a client, the client will be able to view this update in a subsequent read, no matter which replica it reads from. Furthermore, it provides increased durability, since the update will not be lost, even if the master crashes right after acknowledging the update. However, this technique can make write requests slower, since the master has to wait until responses have been received from all the replicas.

In asynchronous replication, the node can reply to the client as soon as it has performed the update in its local storage, without waiting for responses from the other replicas. This increases performance significantly for write requests, since the client does not pay the penalty of the network requests to the other replicas anymore. However, this comes at a cost of reduced consistency and decreased durability. After a client has received a response for an update request, he might read older (stale) values in a subsequent read, if this operation happens in one of the replicas that has not performed the update yet. On top of that, if the master node crashes right after acknowledging an update and the "propagation" requests to the other replicas are lost, then an update that has been acknowledged is eventually lost. The difference between these 2 techniques is visualised in Figure 7.

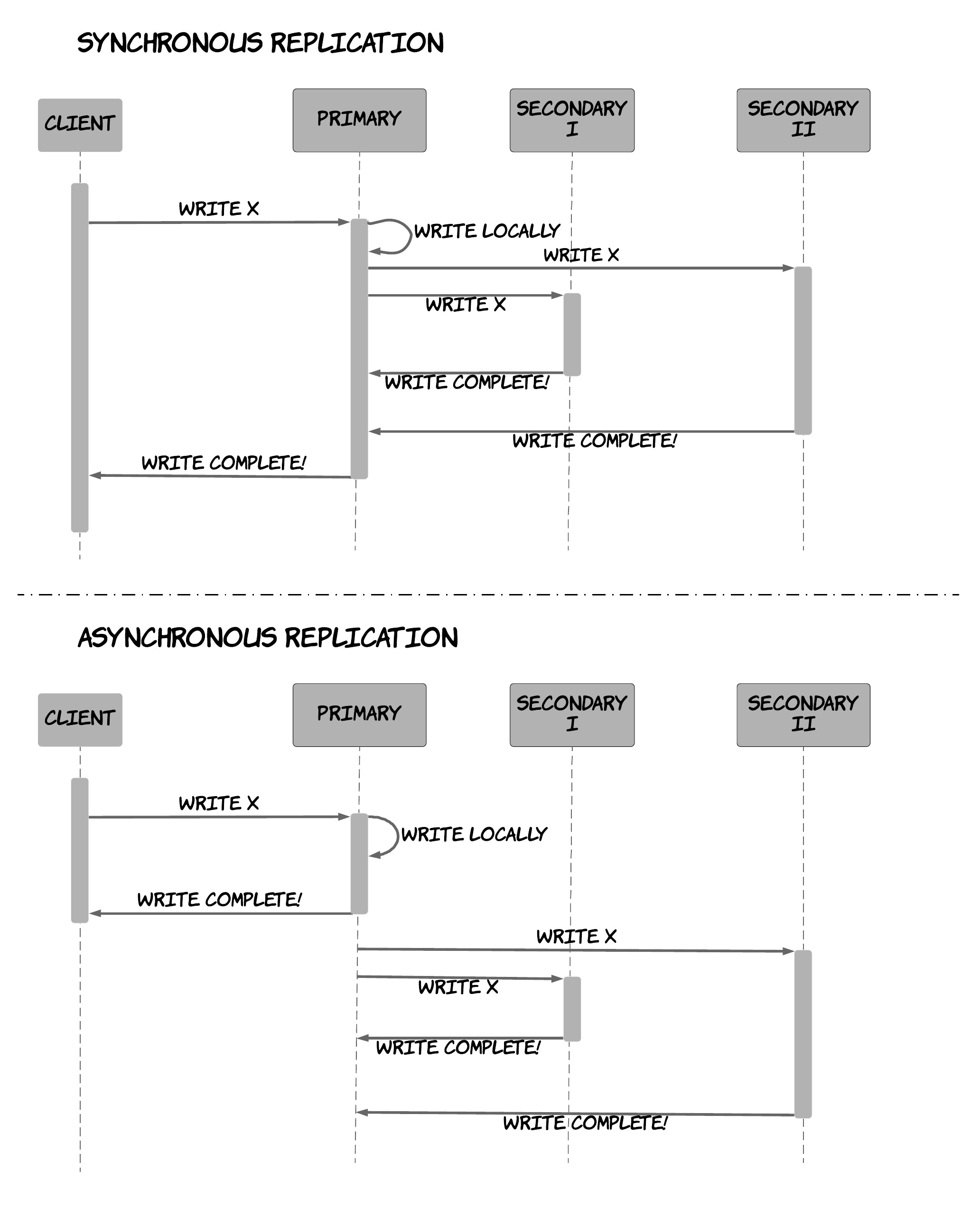
Figure 7: Synchronous vs asynchronous replication

The main advantages of single-master replication are:

• it's simple to understand and to implement.
• concurrent operations are serialized in the master node, obviating the need for more complicated, distributed concurrency protocols. In general, this property also makes it easier to support transactional operations.
• it's quite scalable for workloads that are read-heavy, since capacity for read requests can be increased, by adding more read replicas.

Its main disadvantages are:

• it's not very scalable for write-heavy workloads, since the capacity for writes is determined by the capacity of a single node (the master).
• it imposes an obvious trade-off between performance, durability and consistency.
• failing over to a slave node, when the master node crashes is not instant, it might create some downtime and it also introduces risk of errors. In general, there are two different approaches for performing the failover: manual or automated. In the manual approach, the operator selects the new master node and instructs all the nodes accordingly. This is the safest approach, but it can also incur a significant downtime. The alternative is an automated approach, where slave nodes detect that the master node has crashed (e.g. via periodic heartbeats) and attempt to elect a new master node. This can be faster, but it's also quite risky, because there are many different ways in which the nodes can get confused and arrive to an incorrect state. The chapter about consensus will be covering in more detail this topic, called leader election.
• even though read capacity can be scaled by adding more slave nodes, the network bandwidth of the master node can end up being a bottleneck, if there's a big number of slaves listening for updates. An interesting variation of single-master replication that mitigates this problem is a technique, called chain replication, where nodes form a chain, propagating the updates linearly [10].

Most of the widely used databases, such as PostgreSQL ¹² or MySQL, ¹³ use a single-master replication technique, supporting both asynchronous and synchronous replication.

Multi-master replication

As we've seen in the previous section, the single-master replication is a technique, which is easy to implement and operate, it can easily support transactions and can hide the distributed nature of the underlying system (i.e. when using synchronous replication). However, it has some limitations in terms of performance, scalability and availability. As we've already discussed, there are some kinds of applications, where availability and performance is much more important than data consistency or transactional semantics. A frequently cited example is that of an e-commerce shopping cart, where the most important thing is for the customers to be able to access their cart at all times and be able to add items in a quick and easy way. Compromising consistency to achieve this is acceptable, as long as there is data reconciliation at some point. For instance, if 2 replicas diverge because of intermittent failures, the customer can still resolve any conflicts, during the checkout process.

Multi-master replication is an alternative replication technique that favors higher availability and performance over data consistency ¹⁴. In this technique, all replicas are considered to be equal and can accept write requests, being also responsible for propagating the data modifications to the rest of the group. There is a significant difference with the single-master replication; in multi-master replication, there is no single, master node that serializes the requests imposing a single order, since write requests are concurrently handled by all the nodes. This means that nodes might disagree on what the right order is for some requests. This is usually referred to as a conflict. In order for the system to remain operational when this happens, the nodes need to resolve this conflict, agreeing on a single order amongst the available ones. Figure 8 shows an example, where 2 write requests can potentially result in a conflict, depending on the latency of the propagation requests between the nodes of the system. In the first diagram, write requests are processed in the same order in all the nodes, so there is no conflict. In the second diagram, the write requests are processed in different order in the various nodes (because of network delays), which results in a conflict. In this case, a subsequent read request could receive different results, depending on the node that handles the request, unless we resolve the conflict so that all the nodes converge again to a single value.

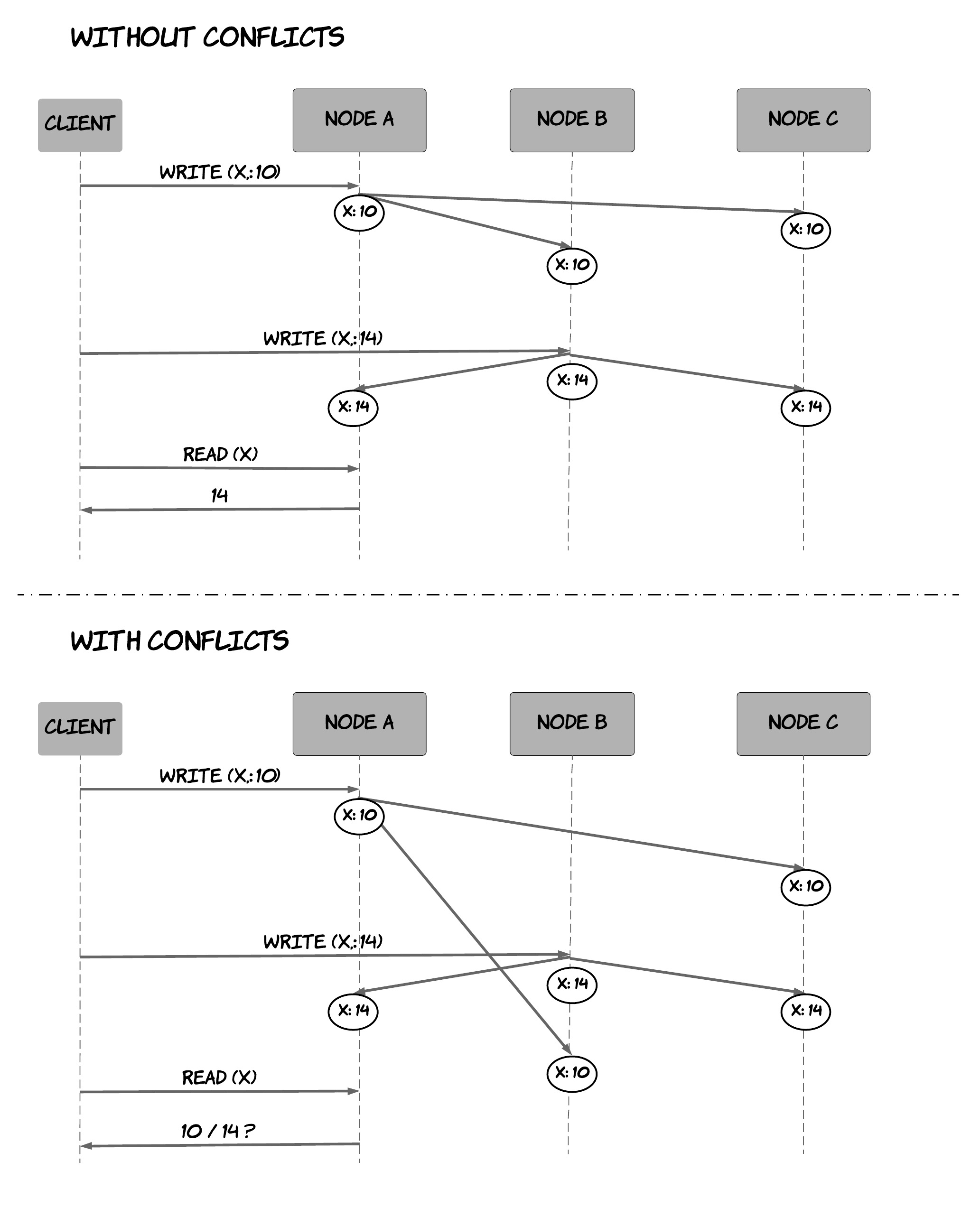
Figure 8: Conflicts in multi-master replication

There are many different ways to resolve conflicts, depending on the guarantees the system wants to provide. An important characteristic of different approaches to resolving conflicts is whether they resolve the conflict eagerly or lazily. In the first case, the conflict is resolved during the write operation. In the second case, the write operation proceeds maintaining multiple, alternative versions of the data record and these are eventually resolved to a single version later on, i.e. during a subsequent read operation. For instance, some common approaches for conflict resolution are:

• exposing conflict resolution to the clients. In this approach, when there is a conflict, the multiple available versions are returned to the client, who selects the right version and returns it to the system, resolving the conflict. An example of this could be the shopping cart application, where the customer selects the correct version of his/her cart.
• last-write-wins conflict resolution. In this approach, each node in the system tags each version with a timestamp, using a local clock. During a conflict, the version with the latest timestamp is selected. Since there can't be a global notion of time, as we've discussed, this technique can lead to some unexpected behaviours, such as write A overriding write B, even though B happened "as a result" of A.
• conflict resolution using causality tracking algorithms. In this approach, the system makes use of an algorithm that keeps track of causal relationships between different requests. When there is a conflict between 2 writes (A, B) and one is determined to be the cause of the other one (suppose A is the cause of B), then the resulting write (B) is retained. However, keep in mind that there can still be writes that are not causally related (requests that are actually concurrent), where the system cannot make an easy decision.

We'll elaborate more on some of these approaches later in the chapter about time and order.

Quorums in distributed systems

The main pattern we've seen so far is writes being performed to all the replica nodes, while reads are performed to one of them. Ensuring writes are performed to all of them (synchronously) before replying to the client, we can guarantee that the subsequent reads will have seen all the previous writes regardless of the node that processes the read operation. However, this means that availability is quite low for write operations, since failure of a single node makes the system unable to process writes, until the node has recovered. Of course, the reverse strategy could be used; writing data only to the node that is responsible for processing a write operation, but processing read operations, by reading from all the nodes and returning the latest value. This would increase significantly the availability of writes, but it would decrease the availability of reads at the same time.

A useful mechanism in achieving a balance in this trade-off is using quorums. For instance, in a system of 3 replicas, we could say that writes need to complete in 2 nodes (also known as a quorum of 2), while reads need to retrieve data from 2 nodes. In this way, we could be sure that reads will read the latest value, because at least one of the nodes in the read quorum will be included in the latest write quorum as well. This is based on the fact that in a set of 3 elements, 2 subsets of 2 elements must have at least 1 common element.

This technique was introduced in a past paper [11] as a quorum-based voting protocol for replica control. In general, in a system that has a total of V replicas, every read operation should obtain a read quorum of V _r replicas, while a write operation should obtain a write quorum of V _w replicas, respectively. The values of these quorums should obey the following properties:

• V _r + V _w > V
• V _w > V / 2

The first rule ensures that a data item is not read and written by 2 operations concurrently, as we just described. The second rule ensures that there is at least one node that will receive both 2 write operations and can impose an order on them. Essentially, this means 2 write operations from 2 different operations cannot occur concurrently on the same data item. Both of the rules together guarantee that the associated distributed database behaves as a centralized, one-replica database system. What this means exactly will become more clear in the sections that follow, which provide more formal definitions of various properties of distributed systems.

The concept of a quorum is really useful in distributed systems that are composed of multiple nodes. As we will see later in the book, it has been used extensively in other areas, like distributed transactions or consensus protocols. The concept is intentionally introduced early on in the book, so that it is easier to identify it as a pattern in the following chapters.

Safety guarantees in distributed systems

Since distributed systems involve a lot of complexity, some safety guarantees are used to ensure that the system will behave in specific expected ways. This makes it easier for people to reason about a system and any potential anomalies that can occur, so that they can build proper safeguards to prevent these anomalies from happening. The main safety guarantees that systems provide are around the following two properties:

• atomicity
• isolation
• consistency

The concepts of atomicity and isolation originate from database research and ACID transactions, while by consistency in this book we will mostly refer to the notion of consistency made popular by the CAP theorem. Thus, before going any further it would be useful to have a look at these topics first.

It is interesting to observe that each one of these safety guarantees is tightly related to one of the aforementioned reasons distributed systems are hard. Achieving atomicity is in a distributed system is challenging because of the possibility of partial failures. Achieving consistency is challenging because of the network asynchrony and achieving isolation is also challenging because of the inherent concurrency of distributed systems.

ACID transactions

ACID is a set of properties of database transactions that are used to provide guarantees around the expected behaviour of transactions in the event of errors, power failures etc. More specifically, these properties are:

• Atomicity (A): this property guarantees that a transaction composed of multiple operations is treated as a single unit. This means that either all operations of the transaction are executed or none of them is. This concept of atomicity translates to distributed systems, where the system might need to execute the same operation in multiple nodes of the system in an atomic way, so that the operation is either executed to all the nodes or to none. This topic will be covered more extensively in the chapter about distributed transactions.
• Consistency (C): this property guarantees that a transaction can only transition the database from one valid state to another valid state, maintaining any database invariants. However, these invariants are application-specific and defined by every application accordingly. For example, if an application has a table A with records that refer to records in a table B through a foreign key relationship ¹⁵, the database will prevent a transaction from deleting a record from table A, unless any records in table B referenced from this record have already been deleted. Note that this is not the concept of consistency we will be referring to in the context of distributed systems, that concept will be presented below.
• Isolation (I): this property guarantees that even though transactions might be running concurrently and have data dependencies, the end result will be as if one of them was executing at a time, so that there was no interference between them. This prevents a large number of anomalies that will be discussed later.
• Durability (D): this property guarantees that once a transaction has been committed, it will remain committed even in the case of failure. In the context of single-node, centralised systems, this usually means that completed transactions (and their effects) are recorded in non-volatile storage. In the context of distributed systems, this might mean that transactions need to be durably stored in multiple nodes, so that recovery is possible even in the presence of total failures of a node along with its storage facilities.

The CAP Theorem

The CAP Theorem [12] is one of the most fundamental theorems in the field of distributed systems, outlining an inherent trade-off in the design of distributed systems. It states that it's impossible for a distributed data store to simultaneously provide more than 2 of the following properties:

• Consistency¹⁶: this means that every successful read request will receive the result of the most recent write request.
• Availability: this means that every request receives a non-error response, without any guarantees on whether that reflects the most recent write request.
• Partition Tolerance: this means that the system can continue to operate despite an arbitrary number of messages being dropped by the network between nodes due to a network partition.

It is very important to understand though that partition tolerance is not a property you can abandon. In a distributed system, there is always the risk of a network partition. If this happens, then the system needs to make a decision either to continue operating while compromising data consistency or stop operating, thus compromising availability. However, there is no such thing as trading off partition tolerance in order to maintain both consistency and availability. As a result, what this theorem really states is the following:

"In the presence of a partition, a distributed system can be either consistent or available."

Let's attempt to schematically prove this theorem in a simplistic way. As shown in Figure 9, let's imagine a distributed system consisting of 2 nodes. This distributed system can act as a plain register, holding the value of a variable, called X. Now, let's assume that at some point there is a network failure between the 2 nodes of the system, resulting in a network partition between them. A user of the system is performing a write and then a read - it could also be 2 different users performing the operations. We will examine the case where each operation is processed by a different node of the system. In that case, the system has 2 options: it can either fail one of the operations (breaking the availability property) or it can process both of the operations returning a stale value from the read (breaking the consistency property). It cannot process both of the operations successfully, while also ensuring that the read returns the latest value, which is the one written by the write operation. The reason is that the results of the write cannot be propagated from node A to node B due to the network partition.

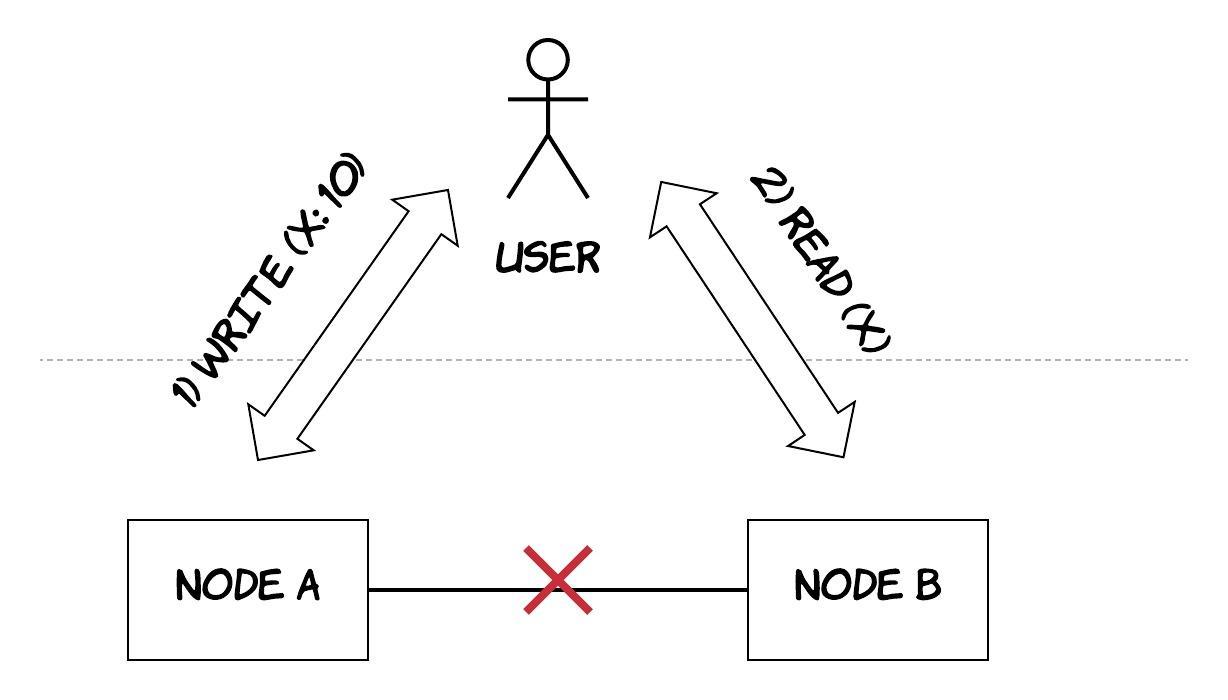
Figure 9: Handling a network partition in a distributed system

This theorem is really important, because it has helped establish this basic limitation that all distributed systems are imposed to. This forced designers of distributed systems to make explicit trade-offs between availability and consistency and engineers become aware about these properties and choose the right system appropriately. When looking at the literature or reading documentation of distributed systems, you will notice systems are usually classified in 2 basic categories, CP and AP, depending on which property the system violates during a network partition. Sometimes, you might even find a third category, called CA. As explained previously, there is no such category for distributed systems and people usually refer either to one of the other two categories instead or to a non-distributed system, such as a single node database.

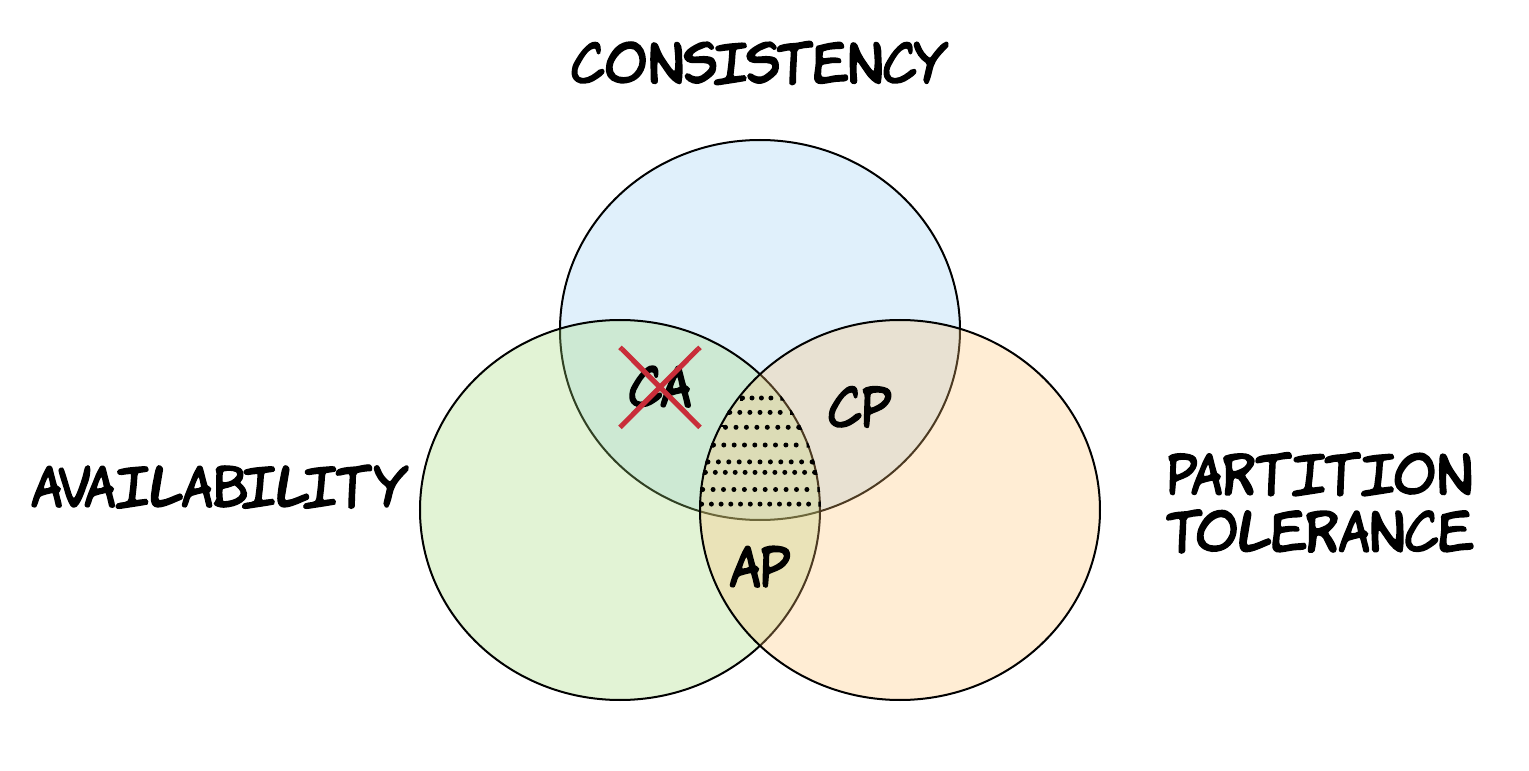
Figure 10: Categories of distributed systems according to the CAP theorem

There is another important thing to note about the CAP theorem: this choice between consistency and availability needs to be made only during a network partition. At all other times, both of these properties can be satisfied. However, even during normal operation when no network partition is present, there's a different trade-off between latency and consistency. In order for the system to guarantee data consistency, it will have to essentially delay write operations until the data have been propagated across the system successfully, thus taking a latency hit. An example of this trade-off is the single-master replication scheme we previously described. In this setting, a synchronous replication approach would favor consistency over latency, while asynchronous replication would benefit from reduced latency at the cost of consistency.

There is actually an extension to the CAP theorem, called the PACELC theorem, captured in a separate article [13]. This theorem states that:

• in the case of a network partition (P), the system has to choose between availability (A) and consistency (C)
• but else (E) when the system is operating normally in the absence of network partitions, the system has to choose between latency (L) and consistency (C).

As a result, each branch of this theorem creates 2 sub-categories of systems. The first part of the theorem defines the two categories we have already seen: AP and CP. The second part defines two new categories: EL and EC. These sub-categories are combined to form 4 categories in total: AP/EL, CP/EL, AP/EC, CP/EC. For instance, a system from the AP/EL category will prioritise availability during a network partition and it will prioritise latency during normal operation. In most of the cases, systems are designed with an overarching principle in mind, which is usually either performance and availability or data consistency. As a result, most of the systems tend to fall into the categories AP/EL or CP/EC. However, there are still systems that cannot be strictly classified in one of these categories, since they have various levers that can be used to tune the system differently when needed. Still, this theorem serves as a good indicator of the various forces at play in a distributed system. You can find a table with the categorisation of several distributed systems along these dimensions in the associated Wikipedia page ¹⁷.

Consistency models

In the previous section, we defined consistency as the property that every successful read request will return the result of the most recent write. In fact, this was an oversimplification, since there are many different forms of consistency. In this section, we will introduce the forms that are the most relevant to the topics of this book.

As with many other things, in order to define what each of these forms really is, one needs to build a formal model. This is usually called a consistency model and it defines the set of execution histories ¹⁸ that are valid in a system amongst all the possible ones. In layman's terms, a model defines formally what behaviours are possible in a distributed system. Consistency models are extremely useful, because they help us formalise the behaviour of a system. Systems can then provide guarantees about their behaviour and software engineers can be confident that the way they use a distributed system (i.e. a distributed database) will not violate any safety properties they care about. In essence, software engineers can treat a distributed system as a black box that provides a set of properties, while remaining unaware of all the complexity that the system assumes internally in order to provide these. We say that a consistency model A is stronger than model B, when the first one allows fewer histories. Alternatively, we could say model A makes more assumptions or poses more restrictions on the possible behaviours of the system. Usually, the stronger the consistency model a system satisfies the easier it is to build an application on top of it, since the developer can rely on stricter guarantees.

There are many different consistency models in the literature. In the context of this book, we will focus on the most fundamental ones, which are the following:

• Linearizability
• Sequential Consistency
• Causal Consistency
• Eventual Consistency

A system that supports the consistency model of linearizability [14] is one, where operations appear to be instantaneous to the external client. This means that they happen at a specific point from the point the client invokes the operation to the point the client receives the acknowledgement by the system the operation has been completed. Furthermore, once an operation is complete and the acknowledgement has been delivered to the client, it is visible to all other clients. This implies that if a client C2 invokes a read operation after a client C1 has received the completion of its write operation, then C2 should see the result of this (or a subsequent) write operation. This property of operations being "instantaneous" and "visible" after they are completed seems obvious, right ? However, as we have discussed previously, there is no such thing as instantaneity in a distributed system. Figure 11 might help you understand why. When thinking about a distributed system as a single node, it seems obvious that every operation happens at a specific instant of time and it's immediately visible to everyone. However, when thinking about the distributed system as a set of cooperating nodes, then it becomes clear that this should not be taken for granted. For instance, the system in the bottom diagram is not linearizable, since T ₄ > T ₃, but still the second client won't observe the read, because it hasn't propagated to the node that processes the read operation yet. To relate this to some of the techniques and principles we've discussed previously, the non-linearizability comes from the use of asynchronous replication. By using a synchronous replication technique, we could make the system linearizable. However, that would mean that the first write operation would have to take longer, until the new value has propagated to the rest of the nodes (remember the latency-consistency trade-off from the PACELC theorem!). As a result, one can realise that linearizability is a very powerful consistency model, which can help us treat complex distributed systems as much simpler, single-node datastores and reason about our applications more efficiently. Moreover, leveraging atomic instructions provided by hardware (such as CAS operations ¹⁹), one can build more sophisticated logic on top of distributed systems, such as mutexes, semaphores, counters etc., which would not be possible under weaker consistency models.

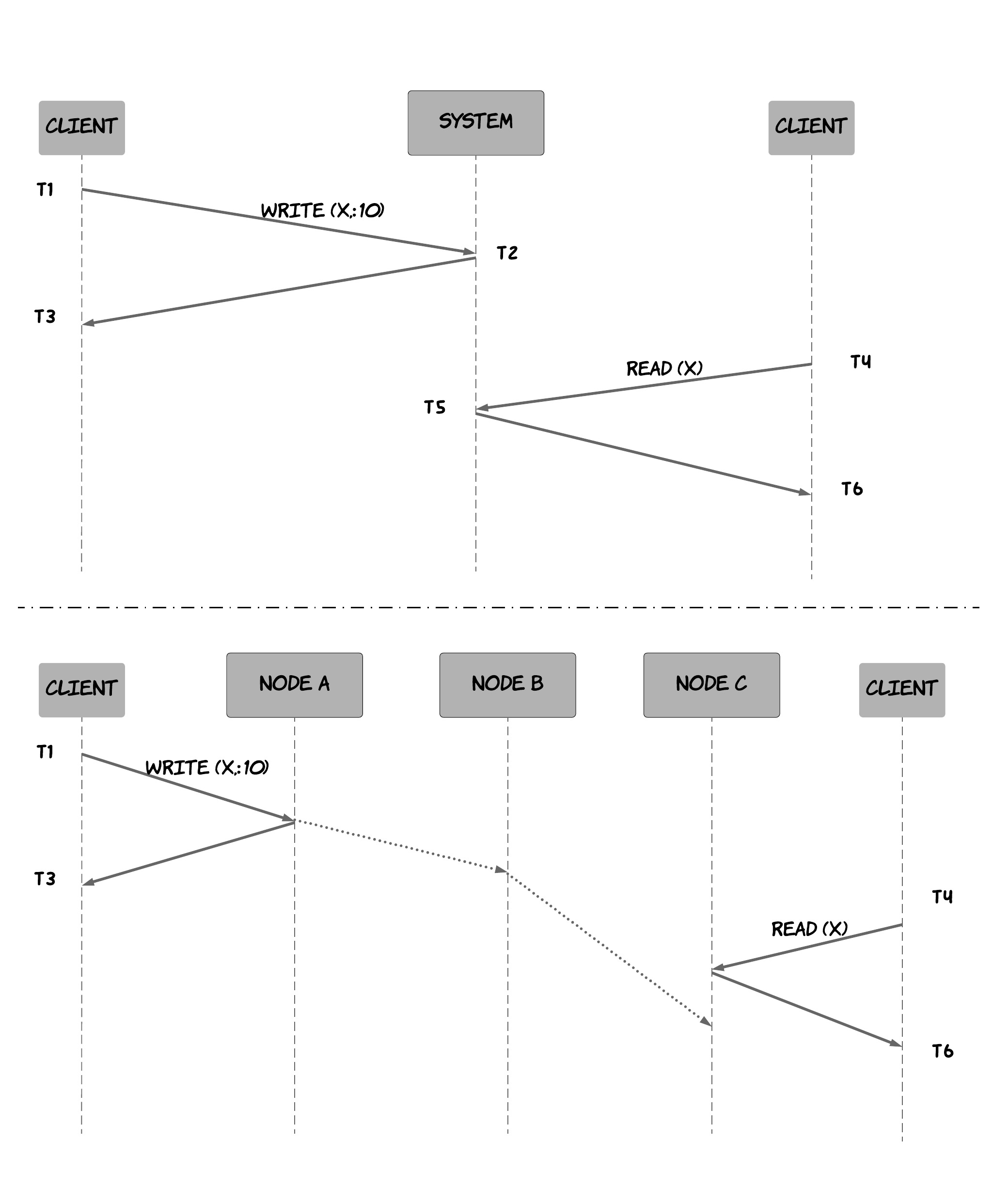
Figure 11: Why linearizability is not obvious in a distributed system

Sequential Consistency is a weaker consistency model, where operations are allowed to take effect before their invocation or after their completion. As a result, it provides no real-time guarantees. However, operations from different clients have to be seen in the same order by all other clients and operations of every single client preserve the order specified by its program (in this "global" order). This allows many more histories than linearizability, but still poses some constraints that can be useful to real-life applications. For example, in a social networking application, one usually does not really care what's the ordering of posts between some of his/her friends, but there's still an expectation that posts from a single friend are displayed in the right order (the one he/she published them at). Following the same logic, one expects his/her comments in a post to appear in the order that he/she submitted them. These are all properties that are captured by this model.

In some cases, we don't even need to preserve this ordering specified by each client's program, as long as causally related operations are displayed in the right order. In our previous example, one could accept comments from one of his/her friends being displayed in a different order than the one he/she originally submitted them, as long as every comment is displayed after the comment it replies to. This would be expected, since there is a cause-and-effect²⁰ relationship between a comment and the comments that constitute replies to it. This is the causal consistency model, which requires that only operations that are causally related need to be seen in the same order by all the nodes. Thus, unlike sequential consistency, the other operations that are not causally related can be seen in different orders in the various clients of the system, also without the need to maintain the order of each client's program. Of course, in order to achieve that each operation needs to contain some information signalling whether it depends on other operations or not. This does not need to be related to time at all and it can be an application-specific property, as in the example we previously described. Causal consistency is one of the weaker forms of consistency, while still preventing a common class of unintuitive behaviours.

There are still even simpler applications that do not have the notion of a cause-and-effect and they would benefit from an even simpler consistency model. For instance, it could be acceptable that the order of operations can be different between the multiple clients of the system and reads do not need to return the latest write, as long as the system eventually arrives at a stable state. In this state, if no more write operations are performed, read operations will return the same result. This is the model of eventual consistency. It is one of the weakest forms of consistency, since it does not really provide any guarantees around the perceived order of operations or the final state the system converges to. It can still be a useful model for some applications, which do not require stronger assumptions or can detect and resolve inconsistencies at the application level.

Note that there are many more consistency models, besides the ones we explained here. ²¹

When explaining the CAP theorem, we encountered the term consistency, but which of all ?

The C property in the CAP theorem refers to the linearizability model we previously described. This means it's impossible to build a system that will be available during a network partition, while also being linearizable. In fact, there has been research that shows that even some weaker forms of consistency, such as sequential consistency, cannot be supported in tandem with availability under a network partition [15].

This vast number of different consistency models creates a significant amount of complexity. As we explained previously, modelling consistency is supposed to help us reason about these systems. However, the explosion of consistency models can have the opposite effect. The CAP theorem can conceptually draw a line between all these consistency models and separate them into 2 major categories: strong consistency models and weak consistency models. Strong consistency models correspond to the C in the CAP theorem and cannot be supported in systems that need to be available during network partitions. On the other hand, weak consistency models are the ones that can be supported, while also preserving availability during a network partition.

Looking at the guarantees provided by several popular distributed systems nowadays (i.e. Apache Cassandra, DynamoDB etc.), there are 2 models that are commonly supported. The first one is strong consistency, specifically linearizability. The second one is weak consistency, specifically eventual consistency. Most probably, the reasons most of the systems converged to these 2 models are the following:

• Linearizability was selected amongst the available strong consistency models, because in order to support a strong consistency model, a system needs to give up availability, as part of the CAP theorem. It then seems reasonable to provide the strongest model amongst the available ones, facilitating the work of the software engineers having to work with it.
• Eventual Consistency was selected amongst the available weak consistency models thanks to its simplicity and performance. Thinking along the same lines, given the application relinquishes the strict guarantees of strong consistency for increased performance, it might as well accept the weakest guarantees possible to get the biggest performance boost it can. This makes it much easier for people designing and building applications on top of distributed systems to make a decision, when deciding which side of the CAP theorem they prefer to build their application on.

Isolation levels

As mentioned already, the inherent concurrency in distributed systems creates the potential for anomalies and unexpected behaviours. Specifically, transactions that are composed of multiple operations and run concurrently can lead to different results depending on how their operations are interleaved. As a result, there is still a need for some formal models that define what is possible and what is not in the behaviour of a system.

These are called isolation levels. We will study the most common ones here which are the following:

• Serializability
• Repeatable read
• Snapshot Isolation
• Read Committed
• Read Uncommitted

Unlike the consistency models presented in the previous section, some of these isolation levels do not define what is possible via some formal specification. Instead, they define what is not possible, i.e. which anomalies are prevented amongst the ones that are already known. Of course, stronger isolation levels prevent more anomalies at the cost of performance. Let's first have a look at the possible anomalies before examining the various levels.

The origin of the isolation levels above and the associated anomalies was essentially the ANSI SQL-92 standard[16]. However, the definitions in this standard were ambiguous and missed some possible anomalies. Subsequent research[17] examines more anomalies extensively and attempts a stricter definition of these levels. The basic parts will be covered in this section, but feel free to refer to it if you are looking for a deeper analysis.

The anomalies covered here are the following:

• Dirty writes
• Dirty reads
• (Fuzzy) non-repeatable reads
• Phantom reads
• Lost updates
• Read skew
• Write skew

A dirty write occurs when a transaction overwrites a value that has previously been written by another transaction that is still in-flight and has not been committed yet. One reason dirty writes are problematic is they can violate integrity constraints. For example, imagine there are 2 transactions A and B, where transaction A is running the operations [x=1, y=1] and transaction B is running the operations [x=2, y=2]. Then, a serial execution of them would always result in a situation where x and y have the same value, but in a concurrent execution where dirty writes are possible this is not necessarily true. An example could be the following execution [x=1, x=2, y=2, commit B, y=1, commit A] that would result in x=2 and y=1. Another problem of dirty writes is they make it impossible for the system to automatically rollback to a previous image of the database. As a result, this is an anomaly that needs to be prevented in most cases.

A dirty read occurs when a transaction reads a value that has been written by another transaction that has not been committed yet. This is problematic, since decisions might be made by the system depending on these values even though the associated transactions might be rolled back subsequently. Even in the case where these transactions eventually commit, this can still be problematic though. An example is the classic scenario of a bank transfer where the total amount of money should be observed to be the same at all times. However, if a transaction A is able to read the balance of two accounts that are involved in a transfer right in the middle of another transaction B that performs the transfer from account 1 to account 2, then it will look like as if some money have been lost from account 1. However, there are a few cases where allowing dirty reads can be useful, if done with care. One such case is to generate a big aggregate report on a full table, when one can tolerate some inaccuracies on the numbers of the report. It can also be useful when troubleshooting an issue and one wants to inspect the state of the database in the middle of an ongoing transaction.

A fuzzy or non-repeatable read occurs when a value is retrieved twice during a transaction (without it being updated in the same transaction) and the value is different. This can lead to problematic situations similar to the example presented above for dirty reads. Other cases where this can lead to problems is if the first read of the value is used for some conditional logic and the second is used in order to update data. In this case, the transaction might be acting on stale data.

A phantom read occurs when a transaction does a predicate-based read and another transaction writes or removes a data item matched by that predicate while the first transaction is still in flight. If that happens, then the first transaction might be acting again on stale data or inconsistent data. For example, let's say transaction A is running 2 queries to calculate the maximum and the average age of a specific set of employees. However, between the 2 queries transaction B is interleaved and inserts a lot of old employees in this set, thus making transaction A return an average that is larger than the maximum! Allowing phantom reads can be safe for an application that is not making use of predicate-based reads, i.e. performing only reads that select records using a primary key.

A lost update occurs when two transactions read the same value and then try to update it to two different values. The end result is that one of the two updates survives, but the process executing the other update is not informed that its update did not take effect, thus called lost update. For instance, imagine a warehouse with various controllers that are used to update the database when new items arrive. The transactions are rather simple, reading the number of items currently in the warehouse, adding the number of new items to this number and then storing the result back to the database. This anomaly could lead to the following problem: transactions A and B read simultaneously the current inventory size (say 100 items), add the number of new items to this (say 5 and 10 respectively) and then store this back to the database. Let's assume that transaction B was the last one to write, this means that the final inventory is 110, instead of 115. Thus, 5 new items were not recorded! See Figure 12 for a visualisation of this example. Depending on the application, it might be safe to allow lost updates in some cases. For example, consider an application that allows multiple administrators to update specific parts of an internal website used by employees of a company. In this case, lost updates might not be that catastrophic, since employees can detect any inaccuracies and inform the administrators to correct them without any serious consequences.

Figure 12: Example of a lost update

A read skew occurs when there are integrity constraints between two data items that seem to be violated because a transaction can only see partial results of another transaction. For example, let's imagine an application that contains a table of persons, where each record represents a person and contains a list of all the friends of this person. The main integrity constraint is that friendships are mutual, so if person B is included in person A's list of friends, then A must also be included in B's list. Everytime someone (say P1) wants to unfriend someone else (say P2), a transaction is executed that removes P2 from P1's list and also removes P1 from P2's list at a single go. Now, let's also assume that some other part of the application allows people to view friends of multiple people at the same time. This is done by a transaction that reads the friends list of these people. If the second transaction reads the friends list of P1 before the first transaction has started, but it reads the friends list of P2 after the second transaction has committed, then it will notice an integrity violation. P2 will be in P1's list of friends, but P1 will not be in P2's list of friends. Note that this case is not a dirty read, since any values written by the first transaction are read only after it has been committed. See Figure 13 for a visualisation of this example. A strict requirement to prevent read skew is quite rare, as you might have guessed already. For example, a common application of this type might allow a user to view the profile of only one person at a time along with his or her friends, thus not having a requirement for the integrity constraint described above.

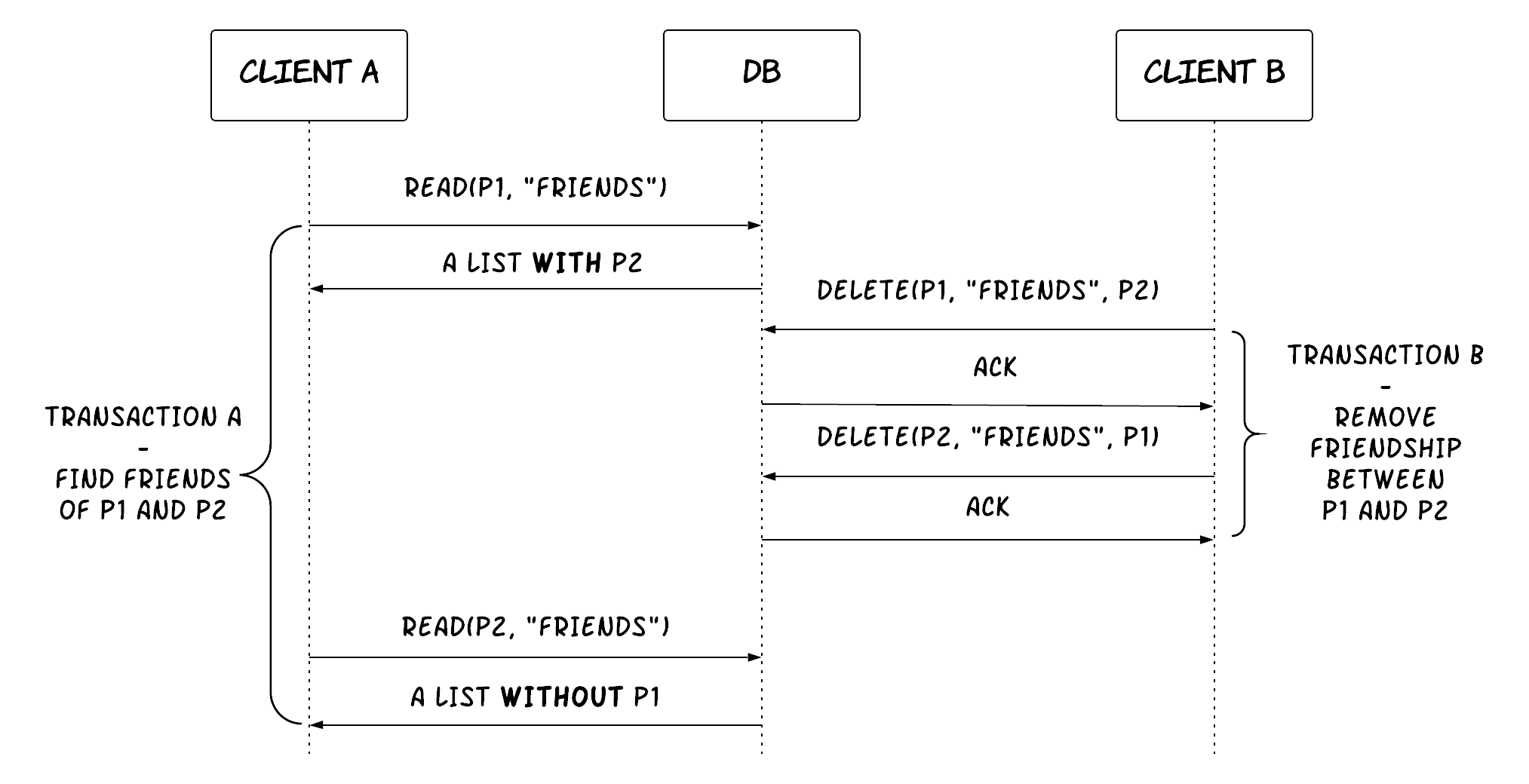
Figure 13: Example of a read skew

A write skew occurs when two transactions read the same data, but then modify disjoint sets of data. For example, imagine of an application that maintains the on-call rota of doctors in a hospital. A table contains one record for every doctor with a field indicating whether they are oncall. The application allows a doctor to remove himself/herself from the on-call rota if another doctor is also registered. This is done via a transaction that reads the number of doctors that are on-call from this table and if the number is greater than one, then it updates the record corresponding to this doctor to not be on-call. Now, let's look at the problems that can arise from write skew phenomena. Let's say two doctors, Alice and Bob, are on-call currently and they both decide to see if they can remove themselves. Two transactions running concurrently might read the state of the database, seeing there are two doctors and removing the associated doctor from being on-call. In the end, the system ends with no doctors being on-call! See Figure 14 for a visualisation of this example.

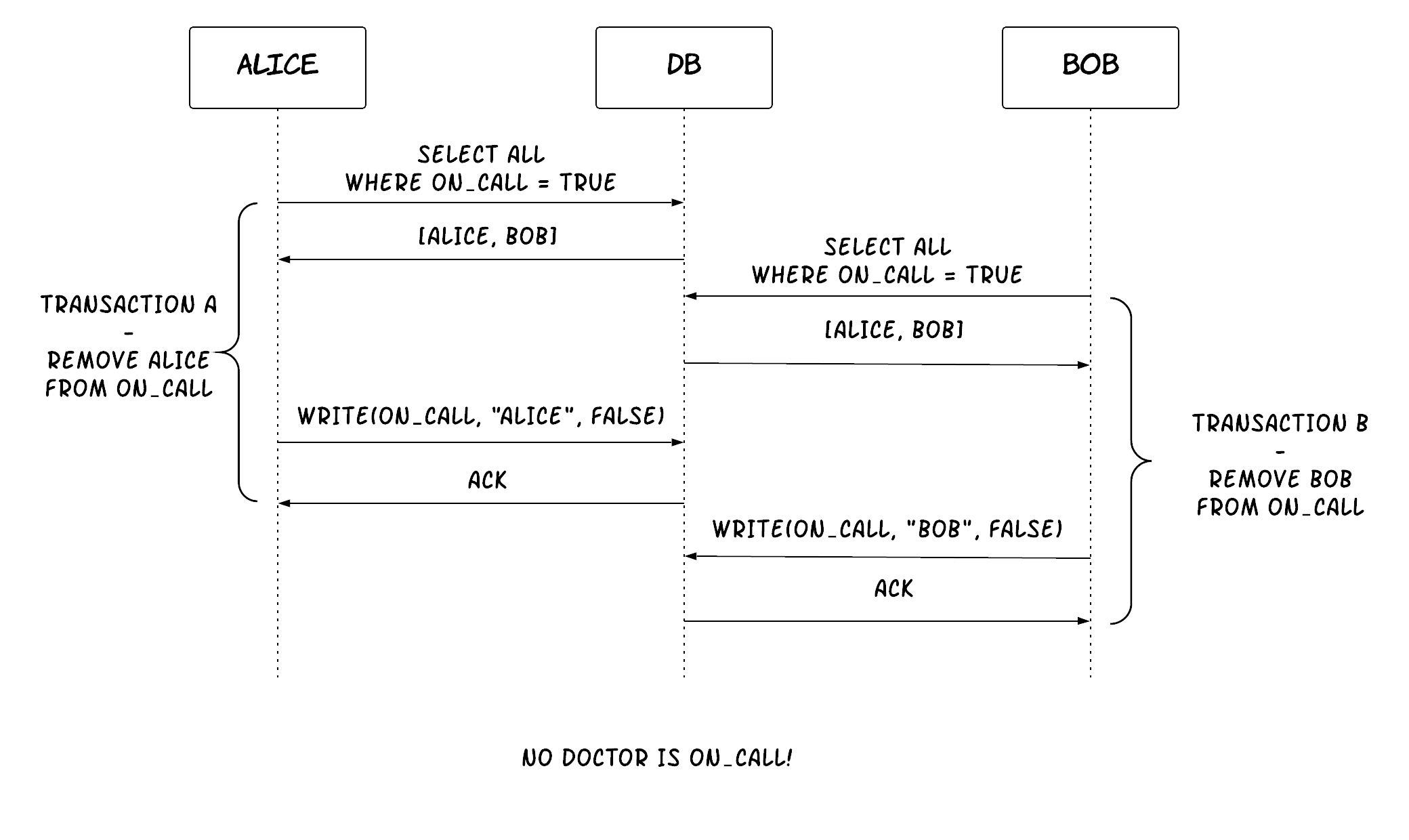
Figure 14: Example of a write skew

It must be obvious by now that there are so many different anomalies to consider. On top of that, different applications manipulate data in different ways, so one would have to analyse each case separately to see which of those anomalies could create problems.

Of course, there is one isolation level that prevents all of these anomalies, the serializable one[18][19]. Similar to the consistency models presented previously, this level provides a more formal specification of what is possible, e.g. which execution histories are possible. More specifically, it guarantees that the result of the execution of concurrent transactions is the same as that produced by some serial execution of the same transactions. This means that one can only analyse serial executions for defects. If all the possible serial executions are safe, then any concurrent execution by a system at the serializable level will also be safe.

However, serializability has performance costs, since it intentionally reduces concurrency to guarantee safety. The other less strict levels provide better performance via increased concurrency at the cost of decreased safety. These models allow some of the anomalies we described previously. Figure 15 contains a table with the most basic isolation levels along with the anomalies they prevent. As mentioned before, these isolation levels originated from the early relational database systems that were not distributed, but they are applicable in distributed datastores too, as shown later in the book.

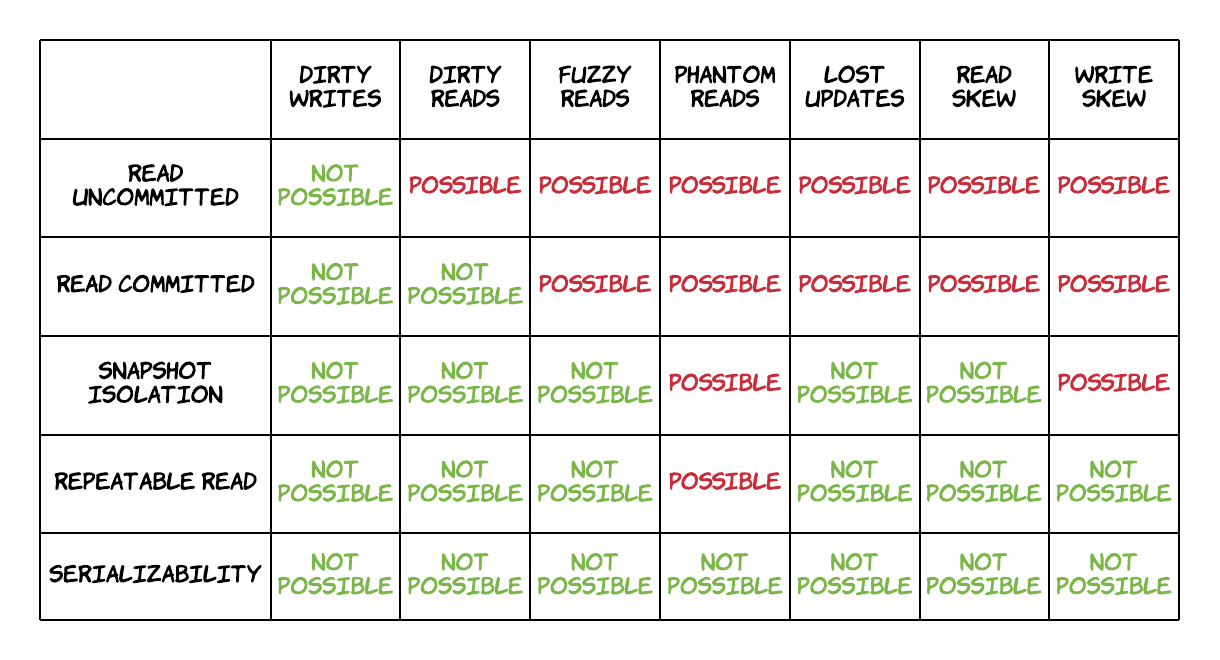
Figure 15: Isolation levels and prevented anomalies

Consistency and Isolation - Differences and Similarities

It is interesting to observe that isolation levels are not that different from consistency models. Both of them are essentially constructs that allow us to express what executions are possible or not possible. In both cases, some of the models are stricter allowing less executions, thus providing increased safety at the cost of reduced performance and availability. For instance, linearizability allows a subset of the executions causal consistency allows, while serializability also allows a subset of the executions snapshot isolation does. This strictness relationship can be expressed in a different way, saying that one model implies another model. For example, the fact that a system provides linearizability automatically implies that the same system also provides causal consistency. Note that there are some models that are not directly comparable, which means neither of them is stricter than the other.

At the same time, consistency models and isolation levels have some differences with regards to the characteristics of the allowed and disallowed behaviours. A main difference between the consistency models and the isolation levels presented so far is that the consistency models applied to single-object operations (e.g. read/write to a single register), while isolation levels applied to multi-object operations (e.g. read & write from/to multiple rows in a table within a transaction). Looking at the strictest models in these two groups, linearizability and serializability, there is another important difference. Linearizability provides real-time guarantees, while serializability does not. This means that linearizability guarantees that the effects of an operation took place at some point between the time the client invoked the operation and the result of the operation was returned to the client. Serializability only guarantees that the effects of multiple transactions will be the same as if they run in a serial order, but it does not provide any guarantee on whether that serial order would be compatible with real-time order.

Figure 16 contains the illustration of an example why real-time guarantees are actually important from an application perspective. Think of an automated teller machine that can support 2 transactions: getBalance() and withdraw(amount). The first transaction performs a single operation to read the balance of an account. The second operation reads the balance of an account, reduces it by the specified amount and then returns to the client the specified amount in cash. Let's also assume this system is serializable. Now, let's examine the following scenario: a customer with an initial balance of x reads his/her balance and then decides to withdraw 20 dollars by executing a withdraw(20) transaction. After the transaction has been completed and the money is returned, the customer performs a getBalance() operation to check the new balance. However, the machine still returns x as the current balance, instead of x-20. Note that this execution is serializable and the end result is as if the machine executed first the getBalance() transactions and then the withdraw(20) transaction in a completely serial order. This example shows why in some cases serializability is not sufficient in itself.

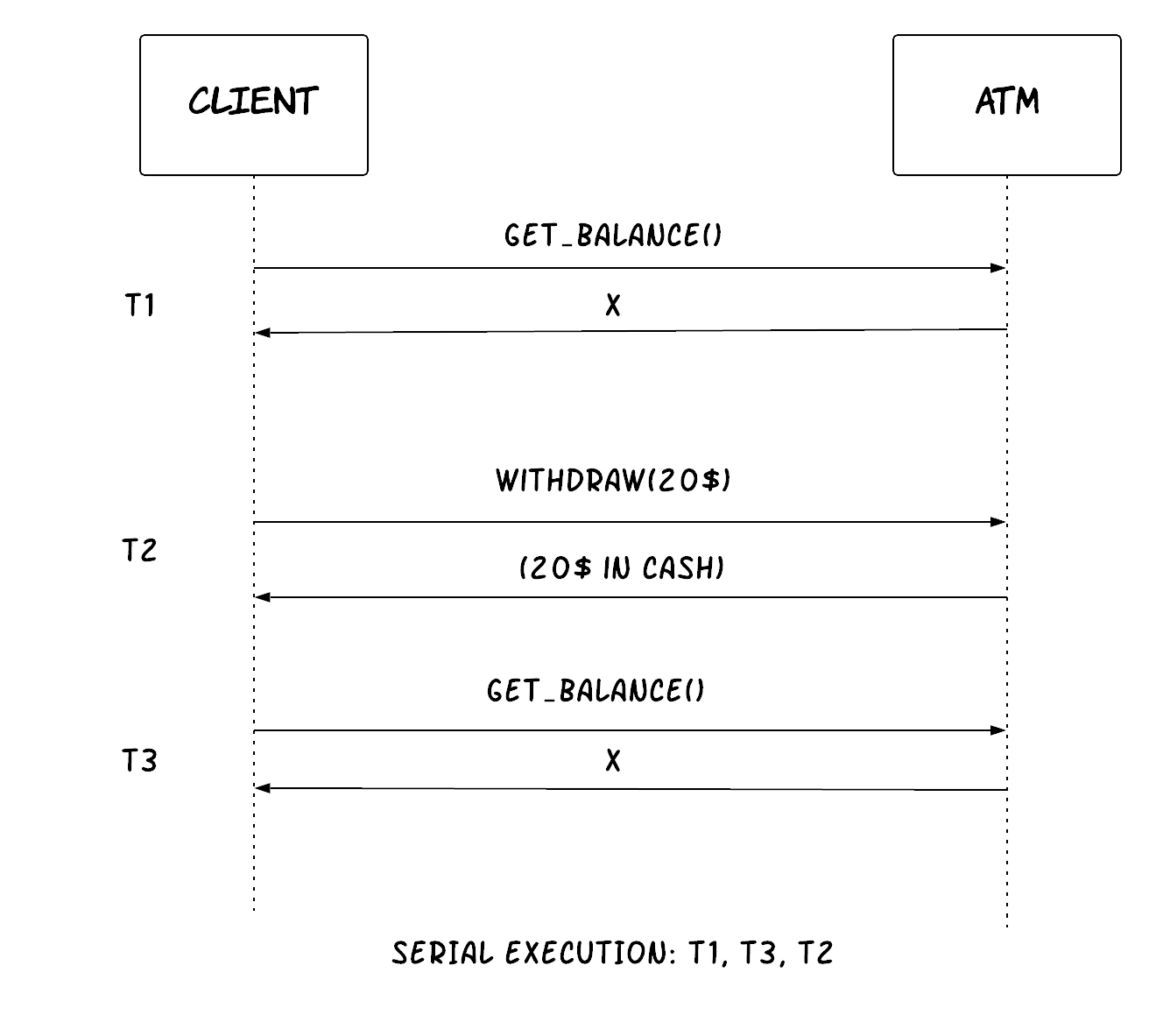
Figure 16: Why serializability is not enough sometimes

In fact, there is another model that is a combination of linearizability and serializability, called strict serializability. This model guarantees that the result of multiple transactions is equivalent to the result of a serial execution of them that would also be compatible with the real-time ordering of these transactions. As a result, transactions appear to execute serially and the effects of each one of them takes place at some point between its invocation and its completion.

As illustated before, strict serializability is often a more useful guarantee than plain serializability. However, in centralized systems providing strict serializability is simple and as efficient as only providing serializability guarantees. As a result, sometimes systems, such as relational databases, advertise serializability guarantees, while they actually provide strict serializability. This is not necessarily true in a distributed database, where providing strict serializability can be more costly, since additional coordination is required. Therefore, it is important to understand the difference between these two guarantees in order to determine which one is needed depending on the application domain.

All of the models presented so far - and many more that were not presented in this book for practical reasons - can be organised in a hierarchical tree according to their strictness and the guarantees they provide. This has actually been done in previous research [15]. Figure 17 contains such a tree containing only the models presented in this book.

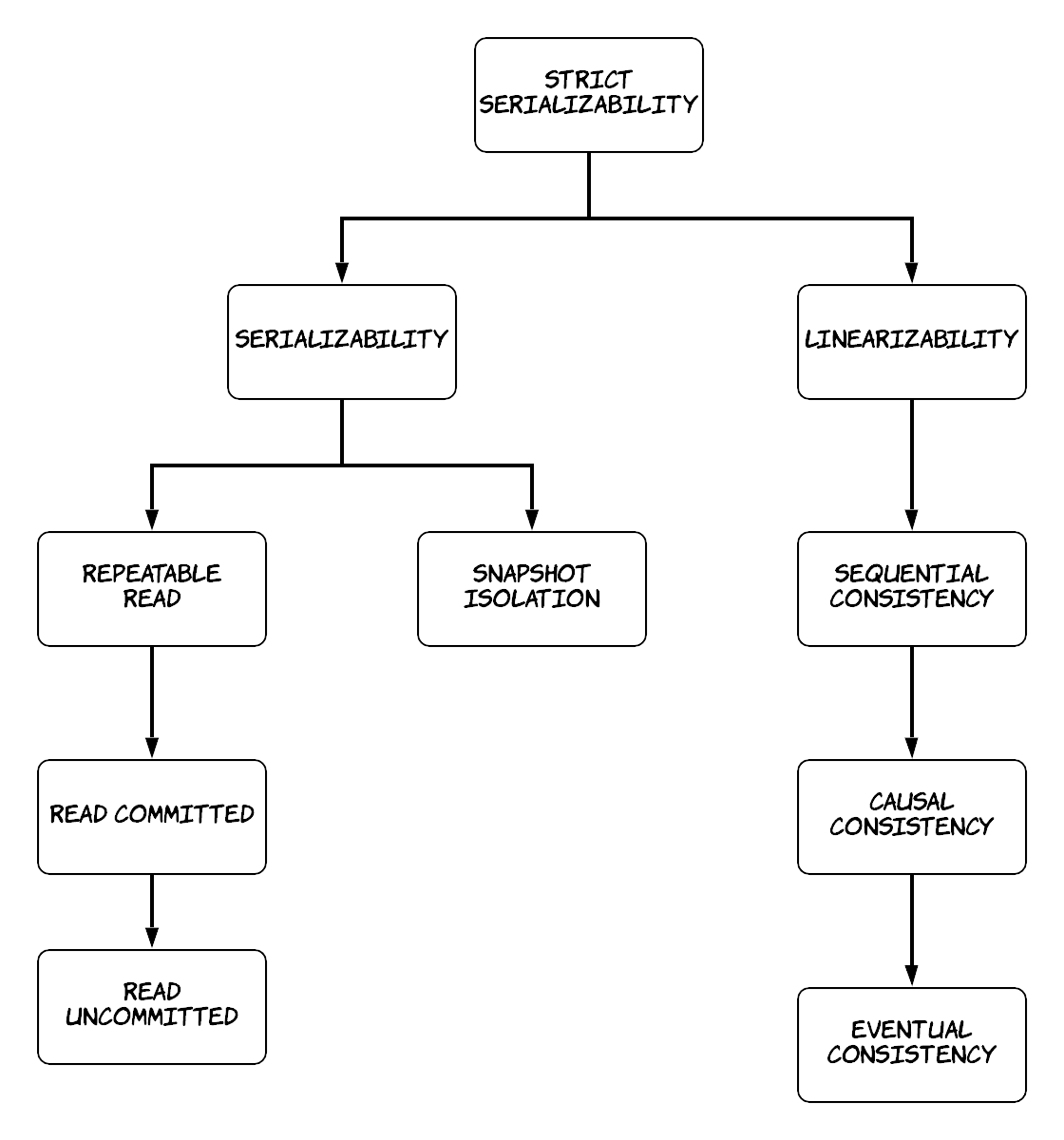
Figure 17: Hierarchy of consistency

Why all the formalities

The previous chapters spent significant amount of time going through many different formal models. But why do we need all these complicated, formal, academic constructs?

As explained before, these constructs help us define different types of properties in a more precise way. As a result, when designing a system it is easier to reason about what kind of properties the system needs to satisfy and which of these models are sufficient to provide the required guarantees. In many cases, applications are built on top of pre-existing datastores and they derive most of their properties from these datastores, since most of the data management is delegated to them. As a consequence, necessary research needs to be done to identify datastores that can provide the guarantees the application needs.

Unfortunately, the terminology presented here and the associated models are not used consistently across the industry making decision making and comparison of systems a lot harder. For example, there are datastores that do not state precisely what kind of consistency guarantees their system can provide or at least these statements are well hidden, while they should be highlighted as one of the most important things in their documentation. In some other cases, this kind of documentation exists, but the various levels presented before are misused leading to a lot of confusion. As mentioned before, one source of this confusion was the initial ANSI-SQL standard. For example, the SERIALIZABLE level provided by Oracle 11g, mySQL 5.7 and postgreSQL 9.0 was not truly serializable and was susceptible to some anomalies.

Understanding the models presented here is a good first step in thinking more carefully when designing systems to reduce risk for errors. You should be willing to search the documentation of systems you consider using to understand what kind of guarantees they provide. Ideally, you should also be able to read between the lines and identify mistakes or incorrect usages of terms. This will help you make more informed decisions. Hopefully, it will also help raise awareness across the industry and encourage vendors of distributed systems to specify the guarantees their system can provide.

1. The approach of scaling a system by adding resources (memory, CPU, disk) to a single node is also referred to as vertical scaling, while the approach of scaling by adding more nodes to the system is referred to as horizontal scaling.

2. See: https://en.wikipedia.org/wiki/Fallacies_of_distributed_computing

3. See: https://grpc.io/

4. See: https://thrift.apache.org/

5. See: https://en.wikipedia.org/wiki/Time_dilation

6. See: https://en.wikipedia.org/wiki/CAS_latency

7. See: https://en.wikipedia.org/wiki/Relational_model

8. See: https://en.wikipedia.org/wiki/Database_normalization

9. See: http://surnamestudies.org.uk/teaching/micro.htm

10. See: https://hbase.apache.org/

11. This technique is also known as primary-backup replication.

12. See: https://www.postgresql.org/

13. See: https://www.mysql.com/

14. This technique is also known as multi-primary replication.

15. See: https://en.wikipedia.org/wiki/Foreign_key

16. As implied earlier, the concept of consistency in the CAP theorem is completely different from the concept of consistency in ACID transactions. The notion of consistency as presented in the CAP theorem is the one that is more important for distributed systems.

17. See: https://en.wikipedia.org/wiki/PACELC_theorem

18. A history is a collection of operations, including their concurrent structure (i.e. the order they are interleaved during execution).

19. See: https://en.wikipedia.org/wiki/Compare-and-swap

20. See: https://en.wikipedia.org/wiki/Causality

21. See: https://en.wikipedia.org/wiki/Consistency_model